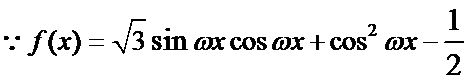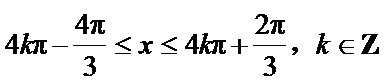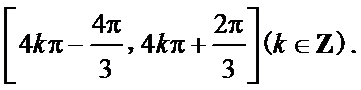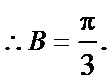- 三角函数中的恒等变换应用
- 共232题
17.已知函数

(1)求函数
(2)在



正确答案
见解析
解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难.
所以,函数

(2)∵ 在

∴ 
∴ 
∵ 
∴ 

∴
又由正弦定理得

∴
考查方向
解题思路
本题考查三角函数问题,解题步骤如下:1、利用辅助角公式及两角和差公式化简求最值。2、利用两角和差公式求解。
易错点
注意角度的范围,忽视则容易出错。
知识点
15.△ABC的三个内角为A、B、C,若

正确答案
1
解析
由题可知,A=45o,可求得tanA=1.本题主要考查了三角函数的公式化简。
考查方向
本题主要考查了三角函数的公式化简。
解题思路
解题步骤如下:利用两角和差公式求解。
易错点
本题要注意公式的化简。
知识点
17.在



(Ⅰ)求证:
(Ⅱ)若


正确答案
见解析
解析
(Ⅰ)
证明:由正弦定理得:
即

(Ⅱ)


考查方向
解题思路
第一问根据正弦定理得到三个角的正弦关系,进而建立角与边的关系,第二问利用正弦定理求面积公式求解
易错点
正弦定理误用、化简整理错误
知识点
17.已知函数f(x)=(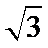
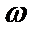
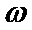
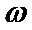
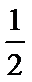
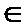
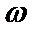
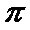
(I)求函数f(x)的单调递增区间;
(II)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
正确答案
(1)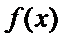
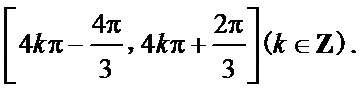
(2)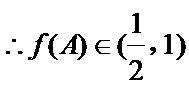
解析
试题分析:本题属于三角函数、解三角形中的基本问题,题目的难度是逐渐由易到难,具体解析如下:
(I)
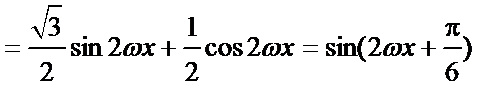
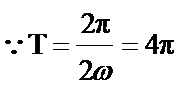
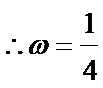
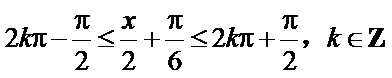
得
∴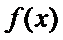
(Ⅱ)由正弦定理得,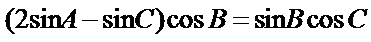

或: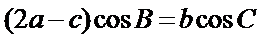
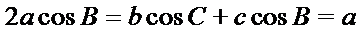
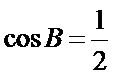
∵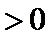
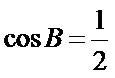
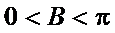
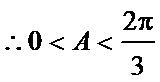

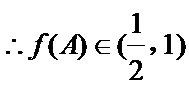
考查方向
本题考查了三角函数的化简与求值,大体可以分成以下几类:
1、由y=Asin(ωx+φ)的部分性质确定其解析式;
2、三角函数的恒等变换及化简求值;
3、正余弦定理的综合运用;
4、三角形中的几何计算;
5、三角函数的最值等.
解题思路
本题考查三角函数以及解三角形,解题步骤如下:
1、化简f(x)=(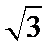

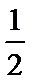
2、求函数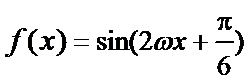
3、根据三角形内角和,利用三角恒等变换求出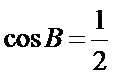
4、利用三角形内角和得出角A的范围,求出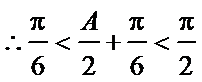
易错点
1、化简f(x)=(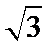
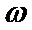

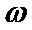

2、求单调区间时候范围不清导致出错;
3、在化简求值时,角的范围不清导致出错。
知识点
6.函数
正确答案
解析
将原函数表达式进行变形得到

然后起单调增区间:
解得

考查方向
解题思路
将原函数表达式进行变形得到
易错点
辅助角公式应用变形错误,不能得到
知识点
扫码查看完整答案与解析