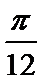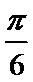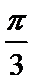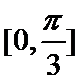- 三角函数中的恒等变换应用
- 共232题
17. 已知函数f(x)=2

(Ⅰ)求函数f(x)的对称轴所在的直线方程;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,且f(C)=3,c=1,ab=2
且a<b,求a,b的值.
正确答案
(1)

解析
试题分析:本题属于简单的三角恒等变换及正余弦定理解三角型的问题,(1)先用辅助角公式化简再进一步求解,(2)利用余弦定理最后再构造方程组来解答。
17解:(Ⅰ)
对称轴所在的直线方程为:
(Ⅱ) 

∴

∴
由


∴



考查方向
解题思路
本题考查简单的三角恒等变换及正余弦定理解三角型,解题步骤如下:(1)先用辅助角公式化简再进一步求解,(2)利用余弦定理最后再构造方程组来解答。
易错点
不会使用辅助角公式合二为一。
知识点
4.将函数f (x) =
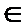
正确答案
解析
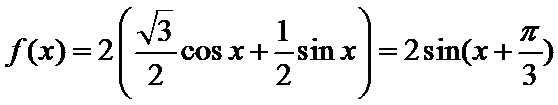
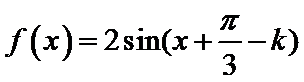
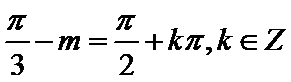
考查方向
解题思路
先利用辅助角公式合二为一,再利用三角函数的性质找出正确答案。
易错点
三角函数的性质。
知识点
10.已知角




正确答案
解析
由角







考查方向
解题思路
先根据题中的条件求出函数的解析式为

易错点
不会转化题中的条件角


知识点
13.函数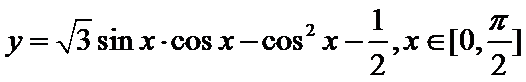
正确答案
解析
试题分析:依题意可知
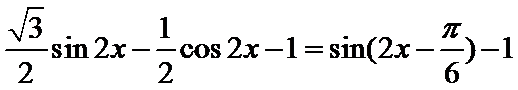
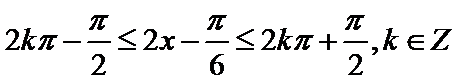
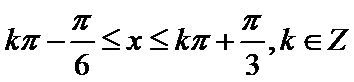
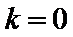
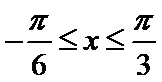
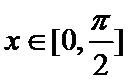
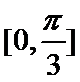
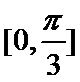
考查方向
解题思路
先化简函数解析式,再求单调区间。
易错点
化简函数解析式时因对三角恒等变换共识不熟悉导致出错。
知识点
13.若

正确答案
解析
试题分析:依题意可知


考查方向
解题思路
直接运用倍角公式及诱导公式即可求解。
易错点
相关知识点不熟悉导致出错。
知识点
扫码查看完整答案与解析