三角函数中的恒等变换应用
共232题

· 三角函数中的恒等变换应用

三角函数中的恒等变换应用
共232题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

设是数列的前项和，点在直线上。

（1）求数列的通项公式；

（2）记，数列的前项和为，求使的的最小值；

（3）设正数数列满足，求数列中的最大项。

正确答案

见解析。

解析

（1）依题意得，则时，

，

又时，，

∴数列是以为首项，以2为公比的等比数列，∴ .

（2）依题意，

由，得

因此n的最小值为1007.

（3）由已知得即，

知识点

三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

已知集合，，则（）

正确答案

解析

略

知识点

三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

已知直线m，n不重合，平面，不重合，下列命题正确的是

A若m，n，m//，n//，则

B若m，m，，则m//n

C若，m，n，则

D若m，n，则

正确答案

解析

略

知识点

三角函数中的恒等变换应用

题型：简答题

简答题 · 13 分

已知函数。

（1）求函数的单调递增区间；

（2）在△ABC中，内角A、B、C的对边分别为a、b、c，已知, ，，求△ABC的面积。

正确答案

（1）

（2）

解析

（1）

…………1分

…………3分

令

…………5分

函数的单调递增区间. …………6分

（2）由，，

因为为内角，由题意知，所以

因此，解得。 …………8分

由正弦定理，得， …………10分

由，由，可得， …………12分

∴。 …………13分

知识点

正弦函数的单调性三角函数中的恒等变换应用解三角形的实际应用

题型：简答题

简答题 · 12 分

已知角的顶点在原点，始边与轴的正半轴重合，终边经过点.

（1）求的值；

（2）若函数，

求函数在区间上的取值范围，

正确答案

见解析。

解析

（1）因为角终边经过点，所以

，， ------------3分

---------6分

（2），--------8分

----10分

，

故：函数在区间上的取值范围是-------12分

知识点

任意角的三角函数的定义三角函数的恒等变换及化简求值正弦函数的定义域和值域三角函数中的恒等变换应用二倍角的正弦

题型：填空题

填空题 · 5 分

在锐角中, ,，，则（）。

正确答案

解析

略

知识点

三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

函数f (x) =的图像相邻的两条对称轴之间的距离是

正确答案

解析

f (x) =cos+ sin

= 2(sincos+ cossin)

= 2sin

∴周期为T =

则相邻的对称轴间的距离为

知识点

正弦函数的对称性三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

在△ABC中， a、b、c分别是角A、B、C的对边,＝（2a＋c，b）,＝(cosB，cosC)，且＝0，（1）求∠B的大小；（2）若b＝，求a＋c的最大值。

正确答案

见解析。

解析

（1）＝（2a＋c）cosB＋bcosC＝0，

由正弦定理 2sinAcosB＋sinCcosB＋sinBcosC＝0，

2sinAcosB＋sin(B＋C)＝0。

sinA(2cosB＋1)＝0。

∵A，B∈(0，π)，∴sinA≠0，cosB＝－，B＝。

（2）3＝a2＋c2－2accos＝(a＋c)2－ac，

(a＋c)2＝3＋ac≤3＋()2，

∴(a＋c)2≤4，a＋c≤2。

∴当且仅当a＝c时，(a＋c)max＝2。

知识点

三角函数中的恒等变换应用正弦定理解三角形的实际应用数量积判断两个平面向量的垂直关系

题型：简答题

简答题 · 13 分

已知函数.

（1）求的值和的最小正周期；

（2）求函数在区间上的最大值和最小值。

正确答案

（1）

（2）；2

解析

（1）………………2分

因为

………………4分

………………6分

………………8分所以的周期为………………9分

（2）当时，，

所以当时，函数取得最小值………………11分

当时，函数取得最大值………………13分

知识点

三角函数的周期性及其求法正弦函数的定义域和值域三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 12 分

已知函数。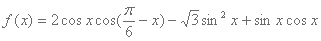

（1）求f（x）的最小正周期；

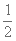
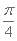
（2）将函数，y＝f（x）的图象上各点的横坐标缩短到原来的倍，纵坐标不变，得到函数，y＝g（x）的图象，求函数g（x）在（0，）上的取值范围。

正确答案

见解析。

解析

知识点

三角函数的周期性及其求法正弦函数的定义域和值域函数y=Asin（ωx+φ）的图象变换三角函数中的恒等变换应用

继续学习学习下一知识点

下一知识点 : 诱导公式的推导

百度题库 > 高考 > 文科数学 > 三角函数中的恒等变换应用

扫码查看完整答案与解析