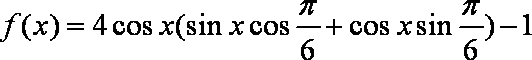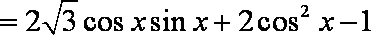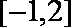三角函数中的恒等变换应用
共232题

· 三角函数中的恒等变换应用

三角函数中的恒等变换应用
共232题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

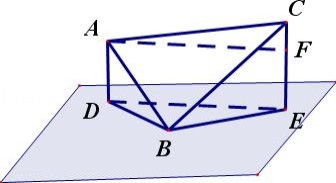
（2005•黑龙江）△ABC的顶点在平面α内，A、C在α的同一侧，AB、BC与α所成的角分别是30°和45°，若AB=3，BC=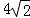，AC=5，则AC与α所成的角为（　　）

A60°

B45°

C30°

D15°

正确答案

解析

作出如图的图形，D是A在面内的射影，E是C在面内的射影过A作AF⊥BC于F直线AC与其在面内射影DE的夹角与角DAE大小相等，求之即可。

解：如图，D是A在面内的射影，

E是C在面内的射影过A作AF⊥BC于F，

则面ADEC与面α垂直，故AC在面内的射影即DE，

直线AC与面α的夹角即AC与DE所成的锐角由作图知，∠CAF的大小即即线面角的大小，

由已知及作图，AB=3，BC=4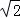，∠ABD=30°，∠CBE=45°

∴AD=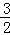，CE=4，

由作图知CF=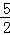，又AC=5，

在直角三角形AFC中，sin∠CAF==，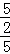

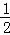
∴∠CAF=30°，即AC与面α所成的角是30°。

故应选C。

知识点

三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

爬山是一种简单有趣的野外运动，有益于身心健康，但要注意安全，准备好必需物品，控制好速度.现有甲、乙两人相约爬山，若甲上山的速度为，下山的速度为（），乙上下山的速度都是（甲、乙两人中途不停歇），则甲、乙两人上下山所用的时间的关系为

A。

D不能确定

正确答案

解析

略

知识点

三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

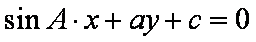
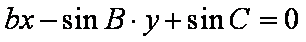
设在三角形ABC中，A、B、C的对边分别为a、b、c，则直线与直线的位置关系是

A垂直

B平行且不重合

C重合

D相交且不垂直

正确答案

解析

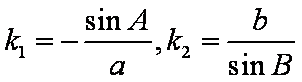
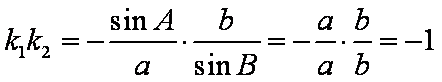
两直线的斜率均存在,则由正弦定理得,故选C

知识点

三角函数中的恒等变换应用

题型：简答题

简答题 · 8 分

已知函数.

（1）求函数的最大值，并指出取得最大值时相应的的值；

（2）求函数的单调增区间。

正确答案

见解析。

解析

（1）

+1+1 ---------------------2分

(注：此处也可是+1等)

所以的最大值是3

此时，即 ----------------------------4分

（2）因为余弦函数的增区间为,

∴ --------------------------6分

∴

∴的单调增区间为 -------------------8分

知识点

正弦函数的单调性三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 12 分

已知函数, .

（1）求函数的最小正周期；

（2）当时，求函数的值域以及函数的单调区间。

正确答案

（1）（2），

解析

解析：

（2）因为，所以 ,所以

函数的增区间为，减区间为

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的单调性三角函数中的恒等变换应用两角和与差的正弦函数

题型：填空题

填空题 · 4 分

设的内角的对边长分别为，且，则的值是___________。

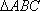
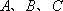
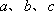
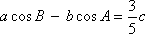
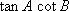
正确答案

解析

略

知识点

三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

已知中，角的对边分别为，，向量，

，且。

（1）求的大小；

（2）当取得最大值时，求角的大小和的面积。

正确答案

见解析

解析

（1）因为，所以

即，因为，所以

所以， 4分

（2）由，

故

由，故最大值时，， 8分

由正弦定理，，得

故， 12分

知识点

三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

已知函数（为常数）。

（1）求函数的最小正周期和单调增区间；

（2）若函数的图像向左平移个单位后，得到函数的图像关于轴对称，求实数的最小值

正确答案

见解析。

解析

（1）

……3分

的最小正周期为 …………4分

当，即时，

函数单调递增，故所求区间为 …………7分

（2）函数的图像向左平移个单位后得，要使的图像关于轴对称，只需 ………9分

即，所以的最小值为，………………12分

知识点

三角函数的周期性及其求法正弦函数的单调性函数y=Asin（ωx+φ）的图象变换三角函数中的恒等变换应用两角和与差的正弦函数

题型：简答题

简答题 · 12 分

已知函数，求在区间上的值域。

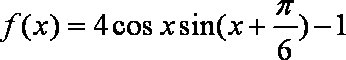
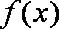
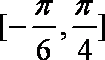
正确答案

见解析。

解析

∵

∴

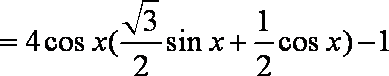
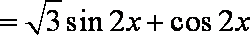
所以，函数在区间的值域是

知识点

正弦函数的定义域和值域三角函数中的恒等变换应用两角和与差的正弦函数

题型：简答题

简答题 · 12 分

若函数的图象与直线相切，相邻切点之间的距离为。

（1）求和的值；

（2）若点是图象的对称中心，且，求点的坐标。

正确答案

见解析。

解析

(1)

由题意知，为的最大值或最小值，所以或由题设知：

函数的周期为所以或，

（2），令，得

，由，得或

因此点的坐标为或

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式三角函数中的恒等变换应用

继续学习学习下一知识点

下一知识点 : 诱导公式的推导

百度题库 > 高考 > 文科数学 > 三角函数中的恒等变换应用

扫码查看完整答案与解析