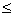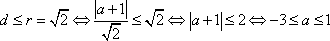- 三角函数中的恒等变换应用
- 共232题
已知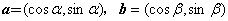
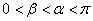
(1)若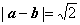
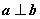
(2)设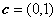
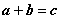
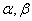
正确答案
见解析
解析
(1)a-b=(cosα-cosβ,sinα-sinβ),
|a-b|2=(cosα-cosβ)2+(sinα-sinβ)2=2-2(cosα·cosβ+sinα·sinβ)=2,
所以,cosα·cosβ+sinα·sinβ=0,
所以,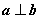
(2)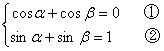
所以,α-β=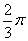
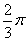
带入②得:sin(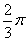
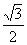
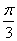
所以,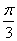
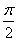
所以,α=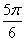
知识点
已知函数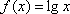
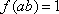
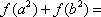
正确答案
2
解析
对数函数题,要求学生会利用对数的运算公式进行化简,同时也要求学生对于基础的对数运算敏感;
知识点
设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式。
正确答案
(1)1; (2) an=3·2n-1-2
解析
(1)由题意有
S1=T1=2S1-1。
故a1=2a1-1。
于是a1=1。
(2)由Tn=2Sn-n2得
Tn-1=2Sn-1-(n-1)2,n≥2。
从而Sn=Tn-Tn-1=2an-(2n-1),n≥2。
由于a1=S1=1,故对一切正整数n都有Sn=2an-(2n-1),①
因此Sn-1=2an-1-(2n-3),n≥2。②
①-②得an=2(an-an-1)-2,n≥2。
于是an=2an-1+2,
故an+2=2(an-1+2),n≥2。
∵a1+2=3,
∴{an+2}是以3为首项,2为公比的等比数列。
∴an=3·2n-1-2
知识点
已知函数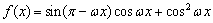
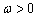
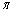
(1)求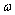
(2)将函数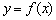

函数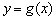
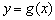
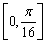
正确答案
见解析。
解析
因此 1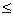
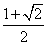
知识点
若直线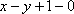
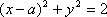

正确答案
解析
圆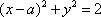
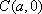
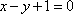
则
知识点
扫码查看完整答案与解析