三角函数中的恒等变换应用
共232题

· 三角函数中的恒等变换应用

三角函数中的恒等变换应用
共232题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知函数.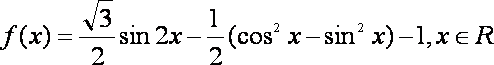

（1）求函数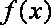的单调递增区间；

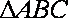
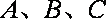
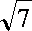
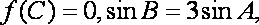
（2）设的内角的对边分别为a、b、c，若c=，求a,b的值

正确答案

见解析。

解析

（1）………………………………4分

……………………………6分

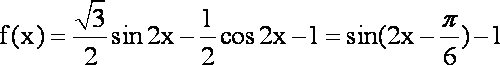
（2）由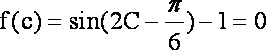得

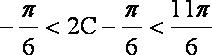
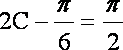
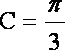
又，所以，即……………………………………8分

由余弦定理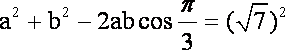①…………………………………………………10分

由得②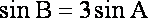

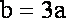
由①②得，a=1,b=3………………………………………………………………………12分

知识点

正弦函数的单调性三角函数中的恒等变换应用正弦定理余弦定理

题型：简答题

简答题 · 10 分

已知是三内角，向量，且

（1）求角.

（2）若，求

正确答案

见解析。

解析

（1）∵, ∴ , 即.

, .

∵, ∴ . ∴.-----------------------5分

（2）由题知，整理得

∴ ∴.

∴或.--------------------------------------------------8分

而使，舍去. ∴.---------------------------10分

知识点

同角三角函数间的基本关系弦切互化三角函数中的恒等变换应用二倍角的正弦数量积的坐标表达式

题型：简答题

简答题 · 10 分

已知数列的前项和，。

（1）求数列的通项公式；

（2）记，求

正确答案

见解析。

解析

（1）当时，，

当时，，

又不适合上式，

∴

（2）∵，

当，

∴

。

知识点

三角函数中的恒等变换应用

题型：简答题

简答题 · 10 分

设

（1）求函数的最小正周期和单调递增区间

（2）当

正确答案

见解析。

解析

（1）……….2分

……………………………….1分

所以函数的单调递增区间是…………………………6分

（2）

…………………………………12分

知识点

三角函数的周期性及其求法正弦函数的单调性三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 8 分

已知，函数

（1）求的最小正周期，并求其图象对称中心的坐标；

（2）当时，求函数f(x)的值域.

正确答案

见解析。

解析

（1）

………2分

所以的最小正周期为

令，得。

故所求对称中心的坐标为- ………4分

（2） ………6分

即的值域为　　 - ………8分

知识点

三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的对称性三角函数中的恒等变换应用数量积的坐标表达式

继续学习学习下一知识点

下一知识点 : 诱导公式的推导

百度题库 > 高考 > 文科数学 > 三角函数中的恒等变换应用

扫码查看完整答案与解析