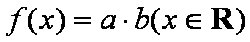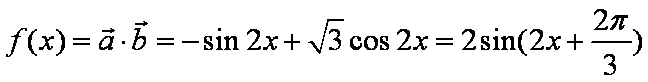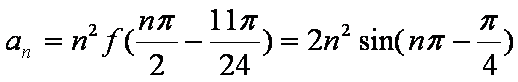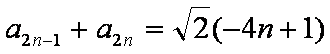- 三角函数中的恒等变换应用
- 共232题
函数f(x)=sin(ωx+φ)(ω>0,|φ|<

正确答案
解析
∵函数f(x)=sin(ωx+φ)的最小正周期是π,
∴ω=
将函数的图象向左平移


由题意,得函数为y=sin(2x+
∴f(0)=sin(


∵|φ|<
故选:C
知识点
已知双曲线




正确答案
解析
解析:由题意得右焦点F(c,0),设一渐近线OA的方程为




解之得:

由FB⊥OB可得,斜率之积等于-1,即

即


故选:D
知识点
已知向量a,b满足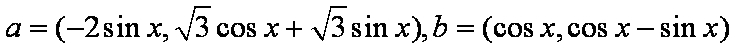
(1)将
(2)已知数列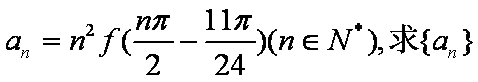
正确答案
见解析。
解析
(1)
(2)
则
所以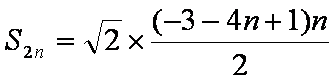
知识点
在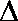
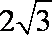
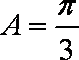
(1)若b=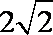
(2)若c=2,求边b的长。
正确答案
(1)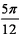
解析
解析:(1)由正弦定理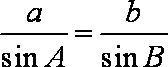
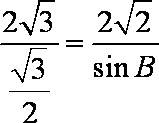
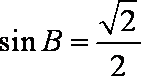
由于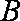
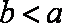
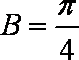
所以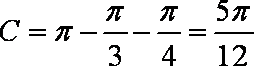
(2)依题意,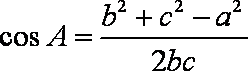
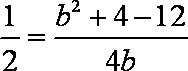
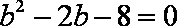
又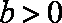
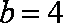
另解:
由于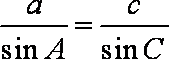
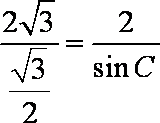
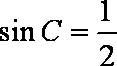
由于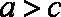
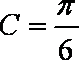
由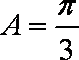
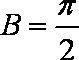
由勾股定理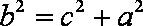
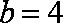
知识点
若直线


正确答案
解析
略
知识点
扫码查看完整答案与解析