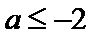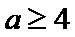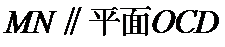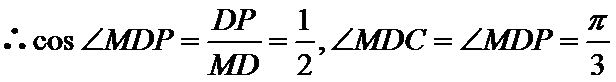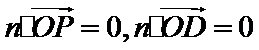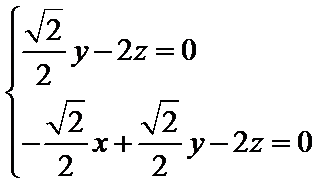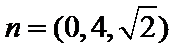- 空间点、线、面的位置关系
- 共260题
19.已知集合 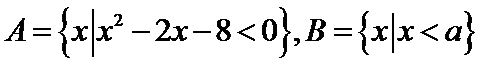
(1)若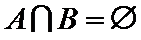
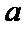
(2)若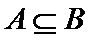
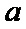
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
5.空间四边形ABCD的两条对角线AC和BD的长分别为6和4,它们所成的角为900,则四边形两组对边中点的距离等于 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在正三角形ABC中,D、E、F分别是AB、BC、AC的中点,G、H、M分别为DE、FC、EF的中点,将
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知以a为首项的数列
(1)若0<

(2)若a,k∈N﹡,求使
(3)若


正确答案
(1)当

当

故
所以当
总有
(2)①当


同理可得,当

当

②当

③当
综上得:当

当

(3)由m


当




解析
解析已在路上飞奔,马上就到!
知识点
6.已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在正方体


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
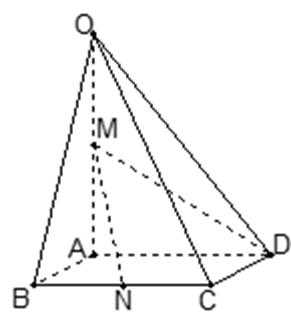
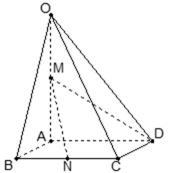
21.如图,在四棱锥









(1)证明:直线
(2)求异面直线

正确答案
方法一(综合法)
(1)取OB中点E,连接ME,NE
又
(2)



连接

所以 

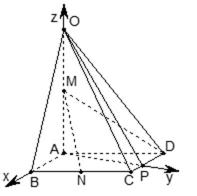
方法二(向量法)作
如图,分别以AB,AP,AO所在直线为

(1)
设平面OCD的法向量为

即

(2)设





解析
解析已在路上飞奔,马上就到!
知识点
20.在直三棱柱








(1)画出此三棱柱的左视图和俯视图;
(2)求三棱锥
正确答案
(1)左视图为正方形
俯视图为直角三角形
(2)








可得:
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,在四棱锥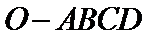
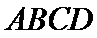
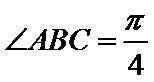
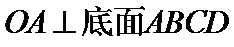
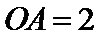
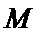

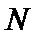
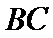
(1)证明:直线
(2)求异面直线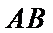
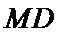
正确答案
方法一(综合法)
(1)取OB中点E,连接ME,NE
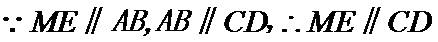
又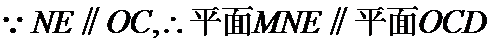
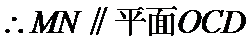
(2)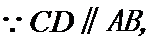
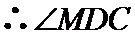
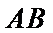
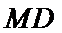


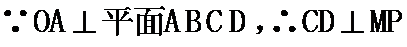
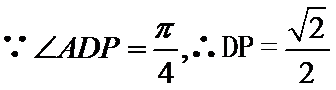
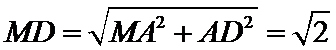
所以 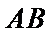
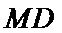
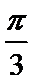
方法二(向量法)作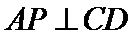
如图,分别以AB,AP,AO所在直线为
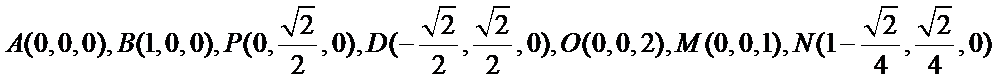
(1)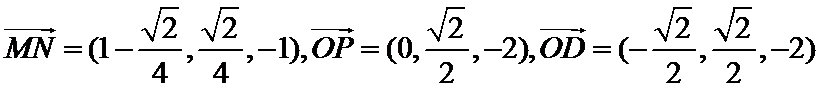
设平面OCD的法向量为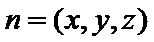
则
即
取
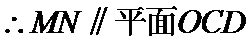
(2)设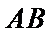
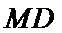

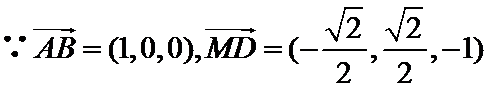
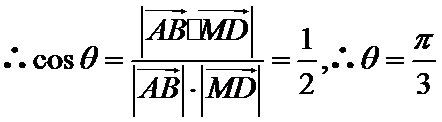
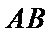
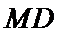
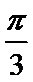
解析
解析已在路上飞奔,马上就到!
知识点
7.如图,正四棱柱



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析