不等式的综合应用
共5题

· 不等式的综合应用

不等式的综合应用
共5题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设直线l1，l2分别是函数f(x)= 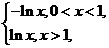图象上点P1，P2处的切线，l1与l2垂直相交于点P，且l1，l2分别与y轴相交于点A，B，则△PAB的面积的取值范围是

A(0,1)

B(0,2)

C(0,+∞)

D(1,+∞)

正确答案

知识点

导数的几何意义不等式的综合应用

题型：填空题

填空题 · 5 分

16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料。生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元。该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为元。

正确答案

216000

知识点

不等式的综合应用

题型：填空题

填空题 · 5 分

14.若，则的最大值是 .

正确答案

解析

由基本不等式得，所以，当且仅当即时取“=”。

考查方向

本题主要考查基本不等式和指数的运算性质等知识，意在考查考生处理数据的能力。

解题思路

利用基本不等式得到；然后化简即可。

易错点

找不到与之间的联系；

知识点

利用基本不等式求最值不等式的综合应用

题型：简答题

简答题 · 12 分

已知均为正数，证明：，并确定为何值时，等号成立。

正确答案

见解析。

解析

（证法一）

因为a，b，c均为正数，由平均值不等式得

①

所以 ②

故.

又 ③

所以原不等式成立.

当且仅当a=b=c时，①式和②式等号成立。当且仅当时，③式等号成立。

即当且仅当a=b=c=时，原式等号成立。

（证法二）

因为a，b，c均为正数，由基本不等式得

所以 ①

同理 ②

故

③

所以原不等式成立.

当且仅当a=b=c时，①式和②式等号成立，当且仅当a=b=c，时，③式等号成立。

即当且仅当a=b=c=时，原式等号成立。

知识点

不等式的综合应用

题型：简答题

简答题 · 12 分

21. 某人上午7：00乘汽车以千米/小时匀速从A地出发到距300公里的B地，在B地不作停留，然后骑摩托车以千米/小时匀速从B地出发到距50公里的C地，计划在当天16：00至21：00到达C地。设乘汽车、骑摩托车的时间分别是x,y小时，如果已知所需的经费元，那么分别是多少时走的最经济，此时花费多少元？

正确答案

解：由题意得，，

∵ ∴

由题设中的限制条件得，

于是得约束条件

目标函数

做出可行域（如图），

当平行移动到过（10，4）点时纵截距最大，此时最小.

所以当，即时，元

解析

解析已在路上飞奔，马上就到！

知识点

其它不等式的解法不等式的综合应用

已学完, 返回章节学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 不等式的综合应用

扫码查看完整答案与解析