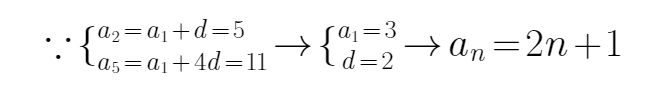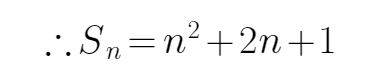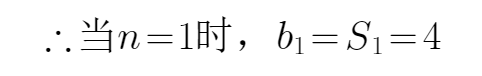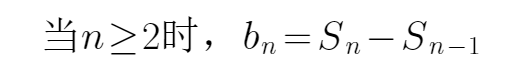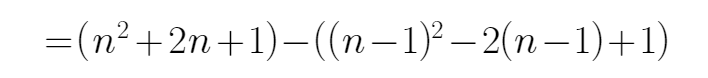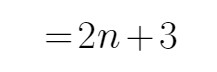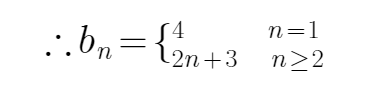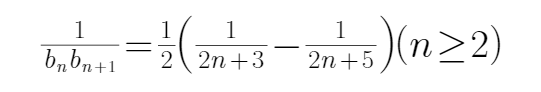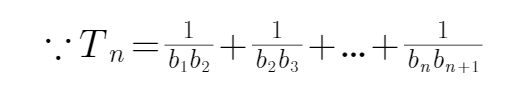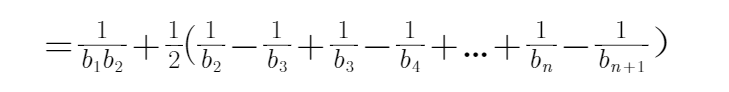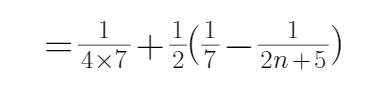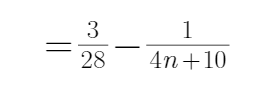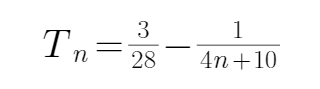- 数列求和、数列的综合应用
- 共491题






17.求{
18.设


正确答案
(Ⅰ)
解析
(Ⅰ)当



当






所以数列{
所以

考查方向
解题思路
(Ⅰ)先用数列第




易错点
本题在用公式法计算通项公式时n=1易丢.
正确答案
(Ⅱ)
解析
(Ⅱ)由(Ⅰ)知,

所以数列{



解题思路
(Ⅱ)根据(Ⅰ)数列{

易错点
本题在裂项中错出现错误。
已知各项均不相等的等差数列



22.求数列


23.是否存在正整数

正确答案
见解析
解析
考查方向
解题思路
借助等差数列前4项和,与
解析式
易错点
本题易错于裂项等号不成立,第二问不理解题意
正确答案
见解析
解析
考查方向
解题思路
根据等比数列性质写出关系式
解不等式确定取值
易错点
本题易错于裂项等号不成立,第二问不理解题意
17. 在等差数列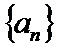

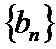
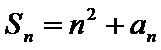
(Ⅰ)求数列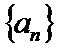
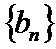
(Ⅱ)求数列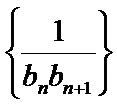
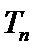
正确答案
见解析
解析
解:
经验证首项不成立
(2)当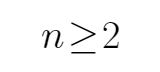
验证: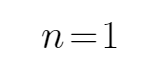
考查方向
主要考察了等差数列的性质及应用,考察了sn与an之间的关系,考察了裂项相消法求和
解题思路
第一步:通过等差数列的性质求出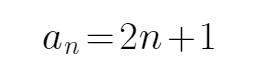
第二步:根据bn的通项公式可知,当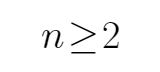
第三步:使用裂项相消的方法得到
易错点
该题在求bn过程中忽略了首项不成立,第二问求Tn的过程中忽略从第二项起,且使用分组的形式书写答案
教师点评
该题主要考察了讨论首项的数列,解题过程中要注意利用前n项和求通项一定要验证首项。
其次,分段数列在求前n项和的时候不需要把n=1独立出来
知识点
已知



19.求数列
20.设




正确答案
an=3或
解析
(Ⅰ)设数列{an}的公比为q,
当

当



综上:an=3或
考查方向
解题思路
设数列{an}的公比为q,根据公比



易错点
容易忽略对
正确答案
解析
证明:若an=3,则bn=0,与题意不符;

考查方向
解题思路
化简

易错点
对于
已知



19.求数列
20.设




正确答案
an=3或
解析
(Ⅰ)设数列{an}的公比为q,
当

当



综上:an=3或
考查方向
解题思路
设数列{an}的公比为q,根据公比



易错点
容易忽略对
正确答案
解析
证明:若an=3,则bn=0,与题意不符;

考查方向
解题思路
化简

易错点
对于
已知在递增等差数列




21.求数列
22.若






正确答案
解析
由










考查方向
解题思路
利用等差数列与等比数列的通项公式即可得出.
易错点
等差、等比数列各自有一些重要公式和性质(略),这些公式和性质是解题的根本,用错了公式和性质,自然就失去了方向。解决这类问题的一个基本出发点就是考虑问题要全面,把各种可能性都考虑进去,认为正确的命题给予证明,认为不正确的命题举出反例予以说明.
正确答案
解析


因为


考查方向
解题思路
存在

易错点
裂项相消的时候易出现多项或少项的情况.
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知数列


正确答案
解析
an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2[1+2+…(n-1)]+33=33+n2-n
所以
设





又因为


知识点
函数


正确答案
解析
因为
知识点
5.定义







正确答案
解析
由“均倒数”为

则
考查方向
本题主要考查数列的综合运算
解题思路
1、求出an;
2、求出bn,利用裂项相消法求和,即可得到结果。
易错点
本题易在求an时发生错误。
知识点
扫码查看完整答案与解析