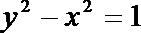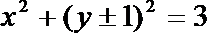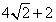- 点到直线的距离公式
- 共25题
20.在平面直角坐标系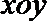
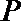
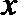
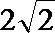
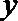
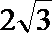
(I)求圆心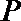
(II)若点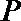
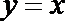
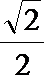
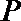
正确答案
(Ⅰ)
(Ⅱ)
解析
解析已在路上飞奔,马上就到!
知识点
11.已知点P(x,y)的坐标满足条件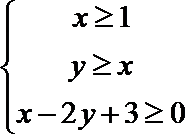
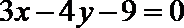
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
4.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
正确答案
解析
如图,由抛物线定义知点P到x=-1的距离即|PF|,由图知|PF|与点P到l1的距离之和的最小值即点F到直线l1的距离,故最小值为
知识点
1.设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为( )
正确答案
解析
由题意知,圆的圆心坐标为(3,-1),圆的半径r=2,|PQ|的最小值为圆心到直线x=-3的距离减去圆的半径长,所以|PQ|min=3-(-3)-2=4.
知识点
22.已知椭圆








(1)设





(2)设



(3)设






正确答案
(1)见解析
(2)
(3)
解析
(1)证明:直线

点C到

因为
所以
(2)解:由

由(1),得

由题意得
解得
(3)设

设
由

同理
由(1)

整理得

由题意知
得
知识点
已知圆C:

正确答案
解析
圆的半径为








知识点
已知圆C:

正确答案
解析
圆的半径为








知识点
极坐标系中,圆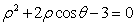
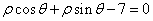
正确答案
解析
将极坐标方程转化成直角坐标方程,圆
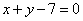
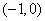
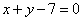
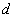
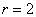
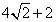
知识点
已知点P在圆x2+y2=1上运动,则P到直线3x+4y+15=0的距离的最小值为 。
正确答案
2
解析
∵x2+y2=1的圆心(0,0),半径为1
圆心到直线的距离为:d=
∴直线3x+4y+15=0与圆相离
∴圆上的点到直线的最小距离为:3﹣1=2
知识点
设



正确答案
解析
略
知识点
扫码查看完整答案与解析