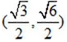对数函数的单调性与特殊点
共20题

· 对数函数的单调性与特殊点

对数函数的单调性与特殊点
共20题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

6．已知函数在其定义域上单调递减，则函数的单调减区间是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性对数函数的单调性与特殊点

题型：填空题

填空题 · 5 分

16．在中，角所对的边分别为且，，若,则的取值范围是____________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点对数函数的单调性与特殊点正弦定理余弦定理平面向量数量积的运算

题型：单选题

单选题 · 5 分

7．函数在上为减函数，则的取值范围是（）

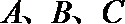
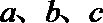
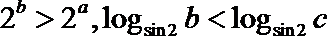
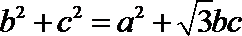
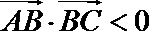
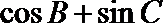
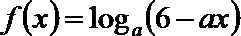
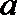
正确答案

解析

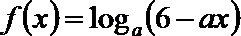
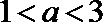
因为函数在上为减函数，则有且，解得，选B．

知识点

复合函数的单调性对数函数的单调性与特殊点

题型：单选题

单选题 · 5 分

3.若 (a>1且a≠2),则a的取值范围为（）

正确答案

解析

当a-1>1,即a>2时,

当0<a-1<1,即1<a<2时,

结合1<a<2,得

知识点

对数的运算性质对数函数的单调性与特殊点其它不等式的解法

题型：单选题

单选题 · 5 分

2.已知函数 (a>0且a≠1),若则x的取值范围为（）

正确答案

解析

由,

即

当a>1时,得ax-1>a,

即,此时

当0<a<1时,得

即,此时

知识点

对数函数的单调性与特殊点其它不等式的解法

题型：单选题

单选题 · 5 分

8.若函数满足的解集是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质对数函数的单调性与特殊点其它不等式的解法

题型：单选题

单选题 · 5 分

5.已知定义在R上的函数f(x)=log2|x-m|-1(m∈R)为偶函数,记a=,b=f(-4),c=f(3+m),则a,b,c的大小关系为(　　).

Aa<b<c

Bc<a<b

Ca<c<b

Dc<b<a

正确答案

解析

由f(x) 为偶函数,得m=0,

所以f(x)=log2|x|-1,

因为,b=f(-4)=log24-1=1,c=f(3)=log23-1<1,

所以a<c<b,

故选C

知识点

函数奇偶性的性质对数函数的单调性与特殊点

题型：填空题

填空题 · 5 分

10.已知函数f(x)=loga(1+x)在区间[1,+∞)上恒有|f(x)|>2,则a的取值范围为　　　　.

正确答案

解析

若a>1,由于在区间[1,+∞)上,

得loga(1+x)>0,

因此，恒成立,

即loga(1+x)>2,得恒成立,

因为2≤x+1,那么a2<2,

结合a>1,得

若0<a<1,由于1+x>1,

得loga(1+x)<0,

因此,|f(x)|>2恒成立,

即

得a-2<x+1恒成立,

因为2≤x+1,那么a-2<2,

结合0<a<1,得<a<1.

综上得,a的取值范围为

知识点

函数恒成立问题对数函数的图像与性质对数函数的单调性与特殊点

题型：单选题

单选题 · 5 分

3.设则实数a的取值范围是（）

Ca>1或

正确答案

解析

当a>1时，

当然

当0<a<1时,

即得

知识点

对数的运算性质对数函数的单调性与特殊点其它不等式的解法

题型：单选题

单选题 · 5 分

3.设a,b,c均为正数,且=log2c,则(　　).

A.a<b<c

B.c<b<a

C.c<a<b

D.b<a<c

正确答案

解析

由题意,画出函数的图象,

从图象可得a<b<c

,故选A.

知识点

指数函数单调性的应用对数值大小的比较对数函数的单调性与特殊点

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 对数函数的单调区间

百度题库 > 高考 > 理科数学 > 对数函数的单调性与特殊点

扫码查看完整答案与解析