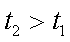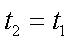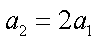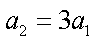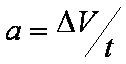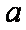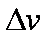- 牛顿第二定律
- 共448题
如图所示,两根竖直放置的足够长的光滑平行金属导轨间距l=0.50m,上端接有阻值R=0.80Ω的定值电阻,导轨的电阻可忽略不计。导轨处于磁感应强度B=0.40T、方向垂直于金属导轨平面向外的有界匀强磁场中,磁场的上边界如图中虚线所示,虚线下方的磁场范围足够大。一根质量m=4.0×10-2kg、电阻r=0.20Ω的金属杆MN,从距磁场上边界h=0.20m高处,由静止开始沿着金属导轨下落。已知金属杆下落过程中始终与两导轨垂直且接触良好,重力加速度g=10m/s2,不计空气阻力。
(1)求金属杆刚进入磁场时通过电阻R的电流大小;
(2)求金属杆刚进入磁场时的加速度大小;
(3)若金属杆进入磁场区域一段时间后开始做匀速直线运动,则金属杆在匀速下落过程中其所受重力对它做功的功率为多大?
正确答案
见解析。
解析
(1)金属杆MN自由下落,设MN刚进入磁场时的速度为v,根据机械能守恒定律,有 
解得 v=
MN刚进入磁场时产生的感应电动势 E=Blv =0.4×0.5×2V=0.40V
通过电阻R的电流大小 I=
(2)MN刚进入磁场时F安=BIl =0.4×0.4×0.5N=0.08N
设MN刚进入磁场时的加速度大小为a,根据牛顿第二运动定律,有
mg - F安=ma
解得 a=8.0m/s2
(3)根据力的平衡条件可知,MN在磁场中匀速下落时有 mg=F安
设MN在磁场中匀速下落时的速度为vm,则此时的感应电动势E=Blvm,感应电流I= Blvm/(R+r),安培力F安=B2l2vm/(R+r)
联立可解得 vm=
在匀速下落过程中重力对金属杆做功的功率P=mgvm=4.0W
知识点
如图,一小球通过两细绳固定在圆环的圆心O位置。已知两绳夹角
正确答案
解析
略
知识点
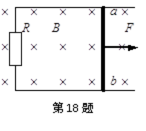
如图,两光滑平行导电导轨水平放置于磁感应强度为B的匀强磁场中,磁场与导轨所在平面垂直,已知金属棒ab能沿导轨自由移动,导轨一端跨接一个定值电阻R,金属棒与导轨电阻均不计,现将金属棒沿导轨以初速度v0开始向右拉动,若保持拉力恒定不变,经过时间t1后金属棒速度变为v,加速度为a1,最终以速度2v做匀速运动,若再使金属棒仍以初速度v0开始,保持拉力的功率不变,经过时间t2后金属棒速度变为v,加速度为a2,最终以速度2v做匀速运动,则
正确答案
解析
略
知识点
对下列物理公式的理解,说法正确的是:
正确答案
解析
略
知识点
如图所示,空间有一场强为E、水平向左的匀强电场,一质量为m、电荷量为+q的滑块(可视为质点)在粗糙绝缘水平面上由静止释放,在电场力的作用下向左做匀加速直线运动,运动位移为L时撤去电场。设滑块在运动过程中,电荷量始终保持不变,已知滑块与水平面间的动摩擦因数为μ。
(1)画出撤去电场前滑块运动过程中的受力示意图,并求出该过程中加速度a的大小;
(2)求滑块位移为L时速度v的大小;
(3)求撤去电场后滑块滑行的距离x。
正确答案
见解析。
解析
(1)滑块沿轨道向左运动过程中的受力如图所示。
根据牛顿运动定律:
又因为
所以 
(2)物块向左做匀加速直线运动,根据运动学公式:
所以 
(3)滑块在导轨运动的整个过程中,根据动能定理有
知识点
如图所示,质量为m的小球A穿在绝缘杆上,细杆的倾角为α,小球A带正电,电荷量为q。在杆上B点处固定一个电荷量为Q的正电荷。将A由距B竖直高度为H处无初速释放,小球A下滑过程中电荷量不变,不计A与细杆间的摩擦,整个装置处于真空中,已知静电力常量k和重力加速度g,求:(1)A球刚释放时的加速度是多大?(2)当A球的动能最大时,A球与B点的距离?(3)若小球到达C点速度最大为v,求A、C两点的电势差UAC?(4)若小球到达D点的速度为0时,A、D两点间的电势差U0,则小球沿杆滑行的位移大小?
正确答案
见解析。
解析
(1)A球刚释放时,受到重力、沿细杆向上的库仑力和细杆的支持力,根据牛顿第二定律得:
得:
(2)到达平衡位置时,速度最大,根据平衡条件,有:
得:
(3)从A到C过程,只有重力和电场力做功,根据动能定理,有:
mgsinα•
将x代入,解得:
(4)从A到D过程,只有重力和电场力做功,设小球沿杆滑行的位移大小为x1,
根据动能定理,有:
mgsinα•x1-q•U0=0

知识点
如图所示,固定的光滑平台上固定有光滑的半圆轨道,轨道半径R=0.6m。平台上静止着两个滑块A、B,mA=0.1Kg,mB=0.2Kg,两滑块间夹有少量炸药,平台右侧有一带挡板的小车,静止在光滑的水平地面上。小车质量为M=0.3Kg,车面与平台的台面等高,车面左侧粗糙部分长度为L=0.8m,动摩擦因数为μ=0.2,右侧拴接一轻质弹簧,弹簧自然长度所在处车面光滑。点燃炸药后,A滑块到达轨道最高点时对轨道的压力大小恰好等于A滑块的重力,滑块B冲上小车。两滑块都可以看作质点,炸药的质量忽略不计,爆炸的时间极短,爆炸后两个物块的速度方向在同一水平直线上,且g=10m/s2。求:
(1)滑块在半圆轨道最低点对轨道的压力
(2)炸药爆炸后滑块B的速度大小
(3)滑块B滑上小车后的运动过程中弹簧的最大弹性势能
正确答案
见解析。
解析
(1)在最高点由牛顿第二定律:
由已知最高点压力
由机械能守恒定律:
在半圆轨道最低点由牛顿第二定律:
解得: 
由牛顿第三定律:
滑块在半圆轨道最低点对轨道的压力大小为7N,方向竖直向下 ……(1分)
(2)由动量守恒定律:

(3)由动量守恒定律:
由能量守恒定律:

知识点
有一质量2kg小球串在长0.5m的轻杆顶部,轻杆与水平方向成
(1)小球下滑的加速度和小球与轻杆之间的动摩擦因数;
(2)如果在竖直平面内给小球施加一个垂直于轻杆方向的恒力,使小球释放后加速度为2m/s2,此恒力大小为多少?
正确答案
见解析
解析
(1)据

另据牛顿第二运动定律有

带入数据可解得
(2)据题意,,根据牛顿第二定律可得:


如果对物体施加垂直与杆子斜向左下方的力F
则有 
解得F=16N
如果对物体施加垂直与杆子斜向右上方的力F

解得
知识点
如图所示,光滑斜面长为a,宽为b,倾角为θ,一物块沿斜面从左上方顶点P水平射入,而从右下方顶点Q离开斜面,此物体在斜面上运动的加速度大小为 ;入射初速度v的大小为 。
正确答案
a = g sinθ, 
解析
略
知识点
14.图示是α粒子(氦原子核)被重金属原子核散射的运动轨迹,M、N、P、Q是轨迹上四点,在散射过程中可以认为重金属原子核静止不动。图中所标出的α粒子在各点处的加速度方向正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析