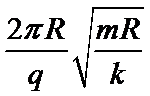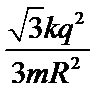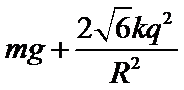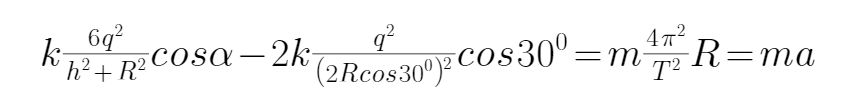- 牛顿第二定律
- 共448题
20.如图甲所示,轻杆一端固定在O点,另一端固定一小球,现让小球在竖直平面内做半径为R的圆周运动。小球运动到最高点时,杆与小球间弹力大小为F,小球在最高点的速度大小为v,其F-v2图象如乙图所示。则( )
正确答案
解析
解:
A、当小球的速度为零时,F=a,则有:F=mg,解得m
B、当v2=b时,杆子的弹力为零,有:

C、由图象可知,v2=b时,杆子的作用力为零,当v2=c>b时,杆子表现为拉力,即杆对小球作用力的方向向下,故C错误.
D、当v2=2b时,根据牛顿第二定律得,

故选:AD
考查方向
匀速圆周运动
解题思路
根据v2=b时,F=0,靠重力提供向心力,结合牛顿第二定律求出当地的重力加速度,根据v=0时,F=a,得出小球的质量.结合牛顿第二定律求出v2=c时杆子作用力的方向,以及v2=2b时,小球的重力与杆子弹力大小的关系.
易错点
要求同学们能根据图象获取有效信息.
知识点
(10分)如图所示,粗糙斜面与光滑水平面通过可忽略的光滑小圆弧平滑连接,斜面倾角α=370.A、B是两个质量均为m=1kg的小滑块(可视为质点),C为左侧附有胶泥的竖直薄板(质量均不计),D是两端分别水平连接B和C的轻质弹簧.当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时,恰能沿斜面向下匀速运动.现撤去F,让滑块A从斜面上距底端L=1m处由静止下滑,求:(g=10m/s2,sin370=0.6)
27.滑块A到达斜面底端时的速度大小;
28.滑块A与C接触粘在一起后,A、B和弹簧构成的系统在作用过程中,弹簧的最大弹性势能.
正确答案
①(5分)
解析
①设




考查方向
动能定理
解题思路
应用平衡条件与动能定理可以求出到达斜面底端的速度.
易错点
关键能正确表示出合外力做的总功.
教师点评
本题考查了动能定理,在近几年的各省高考题出现的频率较高,常与匀变速直线运动规律的综合运用等知识点交汇命题.
正确答案
②(5分)
解析
②当A、B具有共同速度时,系统动能最小,弹簧的弹性势能最大,为
则,
联立以上两式解得:
考查方向
功能关系;动量守恒定律
解题思路
当A、B具有共同速度时,系统动能最小,弹簧的弹性势能最大,根据动量守恒定律与动能定理求解.
易错点
关键通过分析知道当A、B具有共同速度时,弹簧的弹性势能最大.
教师点评
本题考查了功能关系,动量守恒定律,在近几年的各省高考题出现的频率较高,常与功的计算、动能定理等知识点交汇命题.
如图所示,宽L=2m、足够长的金属导轨MN和M′N′放在倾角为θ=30°的斜面上,在N和N′之间连接一个R=2.0Ω的定值电阻,在AA′处放置一根与导轨垂直、质量m=0.8kg、电阻r=2.0Ω的金属杆,杆和导轨间的动摩擦因数μ=
16.中,通过电阻R的电量q;
17.OO′时的速度大小;
18.杆在OO′时,轻绳的拉力大小;
19.上述过程中,若拉力对杆所做的功为13J,求电阻R上的平均电功率。
正确答案
(1)
解析
由法拉第电磁感应定律可知,平均感应电动势为:

代入数据,可得:
考查方向
法拉第电磁感应定律;电量;
解题思路
由法拉第电磁感应定律求出感应电动势、由欧姆定律求出电流、由电流定义式的变形公式求出电荷量.
易错点
关键根据电量公式结合法拉第电磁感应定律解答.
教师点评
本题考查了法拉第电磁感应定律;电量,在近几年的各省高考题出现的频率较高,常与闭合电路欧姆定律等知识点交汇命题.
正确答案
3m/s (4分)
解析
根据题意由几何关系:

杆的速度等于小车速度沿绳方向的分量,由运动合成与分解的知识得:
考查方向
运动的合成和分解
解题思路
根据题意由几何关系求出当杆滑到OO'时轻绳与水平方向的夹角,根据速度合成与分解的知识解答.
易错点
关键是求出当杆滑到OO'时轻绳与水平方向的夹角.
教师点评
本题考查了运动的合成和分解,在近几年的各省高考题出现的频率较高,常与牛顿第二定律、动能定理等知识点交汇命题.
正确答案
12.56N(4分)
解析
杆在OO′时,杆受的摩擦力
杆受的安培力

根据牛顿第二定律:
解得:
考查方向
牛顿第二定律
解题思路
杆在OO′时,对杆进行受力分析,根据牛顿第二定律解答.
易错点
关键是正确对杆进行受力分析,依牛顿第二定律列式.
教师点评
本题考查了牛顿第二定律,在近几年的各省高考题出现的频率较高,常与匀变速直线运动规律的综合运用等知识点交汇命题.
正确答案
2.0W (6分)
解析
根据动能定理:
解出
那么,R上的电热
此过程所用的时间
R上的平均电功率
考查方向
功能关系;功率;
解题思路
根据能量转化关系求出电路上产生的总热量,根据电路连接进而求出电阻上产生的热量,根据功率公式求出电阻上的平均功率.
易错点
关键是求出总热量后根据串并联电路关系得出电阻R上的热量.
教师点评
本题考查了功能关系、功率,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
如图所示,一长L=2m、质量M=4kg的薄木板(厚度不计)静止在粗糙的水平台面上,其右端距平台边缘l= 5m,木板的正中央放有一质量为m=1kg的小物块(可视为质点),已知木板与地面

27.F作用了1.2s时,木板的右端离平台边缘的距离;
28.要使小物块最终不能从平台上滑出去,则物块与平台间的动摩擦因数
正确答案
0.64m
解析
假设开始时物块与木板会相对滑动,由牛顿第二定律:
对木板:

对物块:

设作用t秒后,小物块恰好从木板左端滑离,则
,解得
在此过程:木板位移
物块位移

在小物块从木板上滑落后的0.2s内,由牛顿第二定律:
对木板:

木板发生的位移
此时木板距平台边缘
考查方向
牛顿第二定律;匀变速直线运动的公式
解题思路
先假设F作用下物块与木板相对滑动,作用的过程中分别对物块和木板受力分析,使用牛顿运动定律列出式子,解得木块、物块的加速度,最后验证假设是否成立;分别考虑物块在木板上运动与物块滑下木板后的运动情况,结合运动规律及牛顿定律列式可以求出木板距平台边缘的距离.
易错点
关键根据牛顿第二定律求出木板与小物块的加速度,判断两者是否相对滑动.
教师点评
本题考查了牛顿第二定律;匀变速直线运动的公式,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
正确答案
解析
小物块滑至平台后,做匀减速直线运动,由牛顿第二定律:
对物块:



联立解得
考查方向
牛顿第二定律;匀变速直线运动的公式
解题思路
物块在平台上运动,受平台对物块的摩擦力作用做匀减速运动,要使物块不滑下平台,则物块滑下木板后在平台上减速运动到速度为零时依然在平台上,临界点是物块运动到平台的最右端时,速度恰好为零。结合运动学规律及牛顿定律可以求解.
易错点
关键由几何关系分析出木板不会从平台上掉下去的条件.
教师点评
本题考查了牛顿第二定律;匀变速直线运动的公式,在近几年的各省高考题出现的频率较高,常与动能定理、匀变速直线运动的图像等知识点交汇命题.
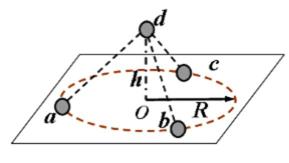
21.如图所示,a、b、c 、d四个质量均为m的带电小球恰好构成“三星拱月”之形,其中a、b、c三 个完全相同的带电小球在光滑绝缘水平面内的同一圆周上绕O点做半径为R的匀速圆周 运动,三小球所在位置恰好将圆周等分。小球d位于O点正上方h处,且在外力F作用下恰处于静止状态,已知a、b、c三小球的电荷量均为q,d球的电荷量为
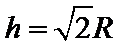
正确答案
解析
A、a、b、c三小球所带电荷量相同,要使三个带电小球做匀速圆周运动,d球与a、b、c三小球一定是异种电荷,由于d球的电性未知,所以a球不一定带正电,故A错误;
BC、设db连线与水平方向的夹角为α,则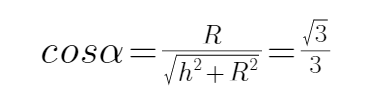
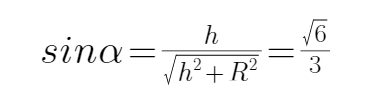
解得: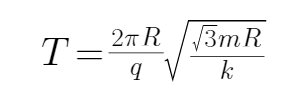
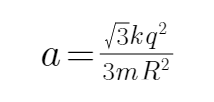
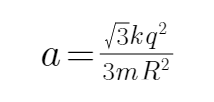
D、对d球,由平衡条件得: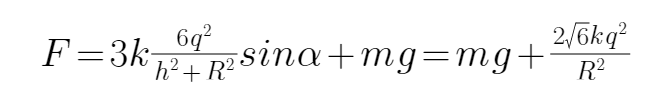
考查方向
电势差与电场强度的关系;库仑定律
解题思路
a、b、c三个带电小球在水平面内做匀速圆周运动,由合外力提供向心力,分析其受力情况,运用牛顿第二定律研究即可.
易错点
关键要正确分析四个小球受力,确定向心力的来源,运用牛顿第二定律和平衡条件研究.
教师点评
本题考查了电势差与电场强度的关系;库仑定律,在近几年的各省高考题出现的频率较高,常与共点力的平衡条件等知识点交汇命题.
知识点
扫码查看完整答案与解析