- 牛顿第二定律
- 共448题
2.关于运动和力的说法中正确的是（ ）
正确答案
解析
A、根据牛顿第二定律可知，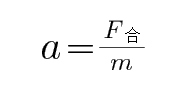
B、合外力不为零，加速度不为零，但是速度仍然可以为零，故B错误；
C、合外力等于零，加速度为零，速度不一定为零，故C错误；
D、合外力越大，加速度越大，速度变化快，但是速度不一定大，故D错误；
考查方向
牛顿第二定律
解题思路
根据牛顿第二定律得出加速度与合力的关系，加速度为零，速度不一定为零.
易错点
关键知道加速度随着合力的变化而变化，大小由合力大小决定，加速度大小与速度之间无必然联系.
知识点
4．用绳子在空中吊一质量为2m的木箱C，其顶部吊一质量为2m的物体A，底部放置一弹
簧，弹簧上端放置质量为m的物体B，整个装置静止。现剪断吊木箱C的绳子，则下列说法正确的是（）
A剪断瞬间A的加速度为零
B剪断瞬间A的加速度为
C剪断瞬间C的加速度为
D剪断瞬间C的加速度为
正确答案
解析
AB.以A为研究对象，在剪断吊木箱C的绳子前，A物体受力平衡加速度为0，在剪断吊木箱C的绳子后，吊A的绳子拉力也是瞬间为0，A只受重力，其加速度为g，故AB错误；
CD.以C为研究对象在剪断吊木箱C的绳子前C受力平衡，合外为为0，C的加速度为0，当剪断吊木箱C的绳子后，A与C没有相互作用，但弹簧形变不能突变，则C受到的合力为3mg，由牛顿第二定律得：3mg=2ma，解得
考查方向
牛顿第二定律
解题思路
分别对A与C在剪断吊木箱C的绳子前后进行受力分析，根据牛顿第二定律解答.
易错点
关键抓住剪断吊木箱C的绳子时，弹簧的长度来不及改变，弹力大小保持不变.
知识点
假设某伞兵做跳伞训练，他从悬停在空中的直升机上由静止跳下，跳离直升机一段时间后打开降落伞做减速下落．若他离地面约为100m时迅速打开降落伞，他打开降落伞后的速度图线如图甲所示，降落伞用8根对称的绳悬挂运动员，每根绳与中轴线的夹角均为37°，如图乙所示．已知人的质量为60kg，降落伞质量为10kg，不计打开降落伞前伞兵下落所受的阻力，打开伞后降落伞所受阻力Ff与速度v成正比，即Ff＝kv，k为阻力系数，求（取g＝10m/s2）：
35.打开降落伞瞬间伞兵的加速度a；
36.为安全起见，每根悬绳至少应能承受多大的拉力；
正确答案
a＝30m/s2，方向竖直向上
解析
当人和降落伞的速度v=5m/s时做匀速运动，则：
kv=（M+m）g，
解得：k=140N•s/m
对整体，根据牛顿第二定律得：
kv0-（M+m）g=（M+m）a，
代入数据解得：a=30m/s2，方向竖直向上
考查方向
牛顿运动定律的综合应用
解题思路
根据人和降落伞一起做匀速运动时，结合此时的速度，根据共点力平衡求出阻力系数．对整体分析，根据牛顿第二定律求出打开伞瞬间的加速度a的大小和方向；
易错点
通过图线能够得出人和降落伞的运动规律，结合共点力平衡和牛顿第二定律进行求解．
正确答案
T＝375N
解析
设每根绳拉力为T，以运动员为研究对象有：
8Tcos30°-（M+m）g=（M+m）a，
T≈375N
由牛顿第三定律得：悬绳能承受的拉力至少为375N．
考查方向
牛顿运动定律的综合应用
解题思路
当加速度最大时，绳子的拉力最大，根据牛顿第二定律求出拉力．
易错点
通过图线能够得出人和降落伞的运动规律，结合共点力平衡和牛顿第二定律进行求解．
25.电磁弹射在军事上有重要的应用，原理可用下述模型说明．如图甲所示，虚线MN右侧存在一个竖直向上的匀强磁场，一边长为L的正方形单匝金属线框abcd放在光滑水平面上，电阻为R，质量为m，ab边在磁场外侧紧靠MN虚线边界处。从t＝0时起磁感应强度B随时间t的变化规律是B＝B0＋kt（k为大于零的常数），金属框将在安培力作用下加速离开磁场.空气阻力忽略不计．则线框穿出磁场过程中通过导线截面的电荷量为_______；若用相同的金属线绕制相同大小的n匝线框，如图乙所示，在线框上加一恒定质量为M的负载物，在t＝0时加速度为_______。
正确答案
B0L2/R，
解析
穿出过程线框中的平均电动势
若用相同的金属线绕制相同大小的n匝线框，t=0时刻产生的感应电动势
线框的总电阻R总=nR ,线框中的电流
t=0时刻线框受到的安培力F=nB0IL
设线框的加速度为a，根据牛顿第二定律有F=（nm+M）a
解得
考查方向
法拉第电磁感应定律; 牛顿第二定律
解题思路
法拉第电磁感应定律求得平均电动势，结合闭合电路欧姆定律，由电量表达式求电量; 先计算出n匝线框中感应电动势，从而计算出安培力的大小，再由牛顿第二定律算出加速度.
易错点
关键闭合电路欧姆定律结合法拉第电磁感应定律求平均感应电流.
知识点
8.磁悬浮列车的运动原理如图所示，在水平面上有两根很长的平行直导轨，导轨间有与导轨垂直且方向相反的匀强磁场B1和B2，B1和B2相互间隔，导轨上有金属框abcd。当磁场B1和B2同时以恒定速度5m/s沿导轨向右匀速运动时，金属框也会沿导轨向右运动。已知两导轨间距L1=0.4m，两种磁场的宽度均为L2，L2=ab，B1＝B2=B=1.0T。金属框的质量m=0.1kg，电阻R=2.0Ω。设金属框受到的阻力与其速度成正比，即f=kv，比例系数k=0. 08 kg/s。则下列说法正确的是 （）（全部选对的得6分，选对但不全的得3分，有错选的得0分。）
A在线框加速的过程中，某时刻线框速度v′=2m/s，此时电路中的感应电动势大小为1.2V
B在线框加速的过程中，某时刻线框速度v′=2m/s，此时线框的加速度a′的大小为8
C金属框的最大速度为4 m/s
D当金属框达到最大速度时，装置消耗的功率为1.6W
正确答案
解析
A选项：线框的两个长边L1均切割磁感线，E=2BL1（v磁场-v）＝2.4V
B选项：动力为安培力，阻力f=kv
F安=4B2L12（v磁场-v）/R
所以a=F合/m=8m/s2.
C选项：当F安=f时，线框匀速运动，所以v=4m/s
D选项：P1=fv；P2=E2/R；P=P2+P2=1.6W
考查方向
电磁驱动，求解动生电动势产生的安培力大小，再受力分析求解平衡和加速度（牛二）；P=Fv
解题思路
A选项：线框的两个长边L1均切割磁感线，E=2BL1（v磁场-v）＝2.4V
B选项：动力为安培力，阻力f=kv
F安=4B2L12（v磁场-v）/R
所以a=F合/m=8m/s2.
C选项：当F安=f时，线框匀速运动，所以v=4m/s
D选项：P1=fv；P2=E2/R；P=P2+P2=1.6W
易错点
两个边切割磁感线；最后功率为电功率与机械功率之和。
教师点评
本题考察比较综合，要求学生具有良好的运动分析能力，而且必须细心。
知识点
扫码查看完整答案与解析