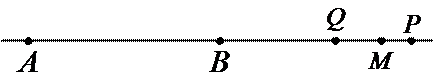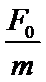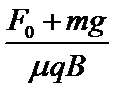- 牛顿第二定律
- 共448题
质量m=4kg的物体，与水平地面间的动摩擦因数μ=0.1，沿水平地面向右做直线运动，经过A点时速度为6m/s。物体过A点时开始计时，对物体施加水平恒力F作用，经过0.5s物体向右移动了2.5m到达B点；若t时刻撤去水平恒力F，物体最后停在A的右方3.75m处。g=10m/s2。求：
28.撤去水平恒力F的时刻t
29.从物体经过A点到最终停止，水平恒力F做的功WF
正确答案
（1） 
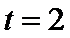
解析
（1）解：首先判断F的方向。设恒力水平向左，大小为F，摩擦力大小为f，物体从A到B的加速度大小为a1。则：由牛顿第二定律：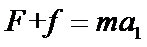
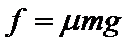
由题设条件，物体从A到B作匀减速运动，有：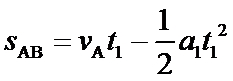
联立并代入数据，得：a1=4m/s2（水平向左），F=12N（水平向左）（1分）
接下来要判断在哪个阶段撤去F。设物体从A点到速度为零的P点共经历的时间为t2，通过的位移为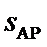
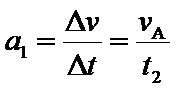
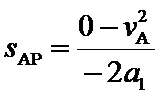
解得：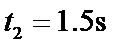
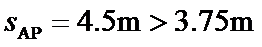
说明物体向右运动阶段没有撤去F
设在t时刻撤去F，则在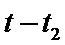
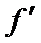
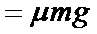
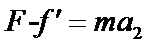
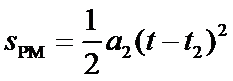
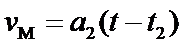
在M点后，物体在摩擦力的作用下匀减速运动到停止在Q点，设其加速度大小为a3，有：
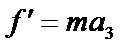
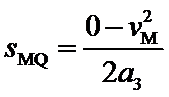
依题意：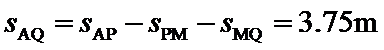
联立并代入数据，得：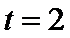
考查方向
牛顿运动定律和运动学公式结合
解题思路
研究AB段，由位移公式求出加速度．再对A到物体停止的整个过程，运用速度位移公式列式，可求得恒力作用的时间．
易错点
知道加速度是联系力学和运动学的桥梁．
正确答案
（2） WF= -51J
解析
（2）根据（1）的分析可知：WF=-F·sAM （2分） 又：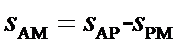
联立并代入数据，得： WF= -51J （2分）
考查方向
动能定理
解题思路
对整个过程，运用动能定理求恒力做功．
易错点
运用动能定理时要灵活选取研究的过程．
如图所示，斜面AB倾角为37°，底端A点与斜面上B点相距10m，甲、乙两物体大小不计，与斜面间的动摩擦因数为0.5，某时刻甲从A点沿斜面以10m／s的初速度滑向B，同时乙物体从B点无初速释放，(sin37°=0.6，cos37°=0.8，g=10m／s2)求：
14.甲物体沿斜面上滑的加速度大小；
15.甲、乙两物体经多长时间相遇．
正确答案
10 m/s2
解析
滑块甲沿斜面向上运动时，加速度大小为a1：
mg（sin 37°+μcos 37°）=ma1
解得：a1=10×（0.6+0.5×0.8）=10 m/s2
考查方向
牛顿第二定律
解题思路
对甲进行受力分析，根据牛顿第二定律求出滑块上滑的加速度.
易错点
关键对甲物体进行正确的受力分析，求出合力.
正确答案
3s
解析
设滑块乙沿斜面向下运动时，加速度大小为a2,根据牛顿第二定律得：
mg（sin 37°-μcos 37°）=ma2
代入数据解得：a2=2 m/s2
滑块甲经
物块乙下滑时的位移大小为：
此时二者之间的距离：△L=L-x1-x2=10-5-1=4m
此时乙的速度为：v=a2t1=2×1=2m/s ,二者还没有相遇，距离是4m两个物块与斜面之间的动摩擦因数相等，所以甲向下运动时的加速度大小也是2m/s2，设再经过t2时间二者相遇，则：
代入数据解得：t2=2s ，所以是乙追上甲，时间为：
考查方向
匀变速直线运动规律的综合运用
解题思路
结合速度时间公式求出速度减为零的时间，求出上滑的最大位移，根据牛顿第二定律求出乙下滑的加速度，根据位移公式求出下滑的位移，从而得出AB两点间的距离；然后再结合几何关系和运动学的公式即可求出相遇的时间.
易错点
关键理清物体在整个过程中的运动规律，结合牛顿第二定律和运动学公式综合求解.
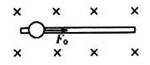
6．如图所示，在垂直纸面向里，磁感应强度为B的匀强磁场中，质量为m，带电量为+q的小球穿在足够长的水平固定绝缘的直杆上处于静止状态，小球与杆间的动摩擦因数为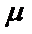
A直杆对小球的弹力方向不变
B直杆对小球的摩擦力先减小后增大
C小球运动的最大加速度为
D小球的最大速度为
正确答案
解析
小球开始滑动时根据牛顿第二定律有：F0-μ（mg-qvB）=ma，随v增大，a增大，当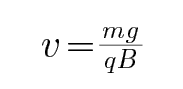
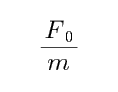
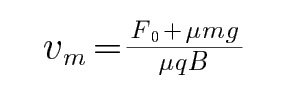
考查方向
运动电荷在磁场中受到的力——洛仑兹力;牛顿第二定律；左手定则
解题思路
小球从静止开始运动，受到重力、支持力、洛伦兹力、摩擦力，根据牛顿第二定律表示出加速度，进而分析出最大速度和最大加速度.
易错点
关键是正确的对小球进行受力分析，抓住当速度增大时，洛伦兹力增大，比较洛伦兹力与重力的大小关系，得出摩擦力的变化情况.
知识点
4．如图3所示，质量相等的A、B小物块用轻弹簧相连，用细线把A悬挂在天花板上，B放在水平面，静止时，B对水平面的压力刚好为零。忽略空气阻力，剪断A上的细线之后
正确答案
解析
A、静止时，B对水平面的压力刚好为零,说明弹簧处于伸长状态，当A向下运动的过程中，弹簧的弹力减小，弹簧的弹力先小于重力，当回复到原长后，继续向下运动过程中，弹力大于重力，所以合力先减小后增大，则A的加速度先减小后增大，故A正确；
B、当A向下运动过程中，弹簧的弹力与重力平衡时速度最大，此时弹簧处于压缩状态，故B错误；
C、A运动到最低点时，A所受的弹力大于其重力，加速度向上，由牛顿第二定律知A处于超重状态，对整体而言，地面对B的支持力大于A、B的重力之和，故C错误；
D、设A、B的质量均为m．细绳剪断前，弹簧伸长的长度为
考查方向
简谐运动的回复力和能量；牛顿第二定律
解题思路
通过分析A的受力情况，由牛顿第二定律分析其加速度如何变化，判断出A的运动情况，确定速度最大的条件．由超重观点，分析地面对B的支持力与两个物体总重力的关系．由简谐运动的对称性分析A运动到最低点时，弹簧的弹性势能与细绳剪断前关系.
易错点
关键分析清楚A的运动情况，运用简谐运动的对称性分析弹簧形变量的关系结合过程解答.
知识点
21．如图，一个质量为m＝1 kg的长木板置于光滑水平地面上，木板上放有质量分别为，mA＝1 kg和mB＝2kg的A、B两物块，A、B两物块与木板之间的动摩擦因数都为μ＝0．2，若现用水平恒力F作用在A物块上，重力加速度g取10 m／s2，滑动摩擦力等于最大静摩擦力，则下列说法正确的是（ ）
A当F＝2N时，A物块和木板开始相对滑
动
B当F＝1 N时，A、B两物块都相对木板静止不动
C若F＝4 N，则B物块所受摩擦力大小为
D若F＝6 N，则B物块的加速度大小为1m／s2
正确答案
解析
A与木板间的最大静摩擦力：fA=μmAg=0.2×1×10N=2N，
B与木板间的最大静摩擦力：fB=μmBg=0.2×2×10N=4N，
A、若F=2N,假定A、B与木板都保持相对静止，整体在F作用下向左匀加速运动，根据牛顿第二定律得：F=(mA+mB)a,代入数据解得a=0.5m/s2,对物块A有：F-f=mAa，解得f=1.5N,所以A物块所受摩擦力f=1.5N＜fA，所以A与木板保持相对静止，故A错误；
B、F=1N＜fA，所以AB相对木板保持相对静止，整体在F作用下向左匀加速运动，故B正确；
C、若F＝4 N，因为F>fA,所以物块A相对木板发生相对滑动，此时B和木板整体受到摩擦力2N,木板质量为1 kg，所以B与木板整体的加速度为
对B进行受力分析，摩擦力提供加速度
D、F=6N＞fA，所以A相对于木板滑动，B和木板整体受到摩擦力2N，B的加速度
考查方向
牛顿第二定律；滑动摩擦力;静摩擦力和最大静摩擦力
解题思路
根据滑动摩擦力公式求出A、B与木板之间的最大静摩擦力，比较拉力和最大静摩擦力之间的关系判断物体的运动情况，进而判断物体所受摩擦力的情况，根据牛顿第二定律求出B的加速度.
易错点
关键是正确对两物体进行受力分析，采用隔离法与整体法根据牛顿第二定律解答.
知识点
扫码查看完整答案与解析