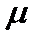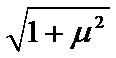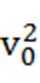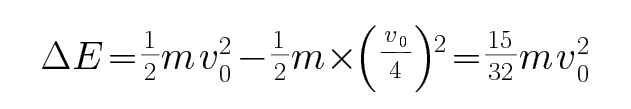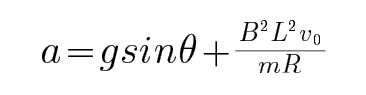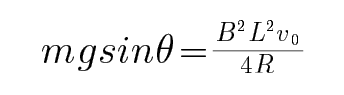- 牛顿第二定律
- 共448题
4.如图,在倾角为α的固定光滑斜面上,有一用绳子栓着的长木板,木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
正确答案
解析
木板沿斜面加速下滑时,猫保持相对斜面的位置不变,即相对斜面静止,加速度为零.将木板和猫作为整体,根据牛顿第二定律F合=F猫+F木板=0+2ma(a为木板的加速度),整体受到的合力的大小为猫和木板沿斜面方向的分力的大小,
即F合=3mgsinα,解得
考查方向
牛顿第二定律
解题思路
对猫和木板受力分析受力分析,可以根据各自的运动状态由牛顿第二定律分别列式来求解,也可以把猫和木板当做一个整体,利用整体法计算.
易错点
关键是对研究对象进行正确的受力分析,应用整体法或隔离法.
知识点
20.在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B,它们的质量分别为m1、m2,弹簧劲度系数为k,C为一固定挡板,系统处于静止状态。现用一平行于斜面向上的恒力F拉物块A使之向上运动,当物块B刚要离开挡板C时,物块A运动的距离为d、速度为v,则此时()
正确答案
解析
A、开始系统处于静止状态,弹簧弹力等于A的重力沿斜面下的分力,当B刚离开C时,弹簧的弹力等于B的重力沿斜面下的分力,故m2gsinθ=kx2,x2为弹簧相对于原长的伸长量,但由于开始是弹簧是压缩的,故d>x2,故m2gsinθ<kd,故A错误;
B、当B刚离开C时,弹簧的弹力等于B的重力沿斜面下的分力,故m2gsinθ=kx2,根据牛顿第二定律:F-m1gsinθ-kx2=ma,已知m1gsinθ=kx1,x1+x2=d 故物块A加速度等于
C、拉力的瞬时功率P=Fv,故C错误;
D、根据功能关系,弹簧弹性势能的增加量等于拉力的功减去系统动能和重力势能的增加量,即为:

考查方向
功的计算;牛顿第二定律;弹性势能
解题思路
当B刚离开C时,弹簧的弹力等于B的重力沿斜面下的分力,根据胡克定律求解出弹簧的伸长量;根据牛顿第二定律求出物块A的加速度大小;根据机械能守恒定律求解A的速度.
易错点
依据弹簧所处的状态,分析物块的位移与弹簧压缩量和伸长量的关系是解题的关键.
知识点
3.一质量为m的木块静止在光滑的水平面上,从t=0开始,将一个大小为F的水平恒力作用在该木块上,在t=t1时刻力F的瞬时功率是( )
正确答案
解析
由牛顿第二定律可以得到,F=ma,所以


考查方向
功率、平均功率和瞬时功率
解题思路
物体做匀加速直线运动,根据牛顿第二定律可以求得物体的加速度的大小,再由速度公式可以求得物体的速度的大小,由P=FV来求得瞬时功率.
易错点
计算平均功率和瞬时功率时一定要注意公式的选择,
知识点
3.如图所示,某杂技演员在做手指玩耍盘子的高难度表演。若盘的质量为m,手指与盘之间的动摩擦因数为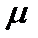
正确答案
解析
A、若手指支撑着盘,使盘保持静止状态,则手指对盘的作用力等于mg,故A错误;
B、若手支撑着盘子一起水平向右匀速运动,合力为零,盘子受重力和支持力,不受静摩擦力,故B错误;
CD、若手支撑着盘子一起水平向右匀加速运动,盘子受重力、支持力和静摩擦力,其中重力和支持力平衡,静摩擦力等于合力,提供加速度,故加速度最大为a=µg;手对盘子的作用力为支持力和静摩擦力的合力,由于f≤μmg,故手对盘子的作用力大小不可超过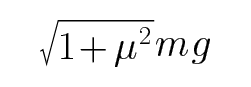
考查方向
牛顿第二定律;静摩擦力和最大静摩擦力
解题思路
若手支撑着盘子一起水平向右匀速运动,盘子受重力和支持力而平衡;若若手支撑着盘子一起水平向右匀加速运动,盘子受重力、支持力和静摩擦力,静摩擦力等于合力,产生加速度,根据牛顿第二定律列式分析.
易错点
已知运动情况分析受力情况,关键是找到加速度的方向,结合牛顿第二定律进行受力分析.
知识点
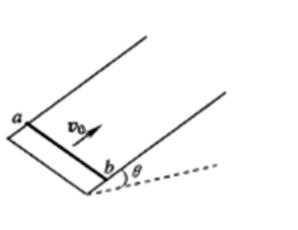
如图所示,质量为m的导体棒垂直放在光滑、足够长的U形导轨底端,导轨宽度和棒长相等且接触良好,导轨平面与水平面成θ角。整个装置处在与导轨平面垂直的匀强磁场中。现给导体棒沿导轨向上的初速度v0,经时间t0,导体棒到达最高点,然后开始返回,到达底端前已做匀速运动,速度大小为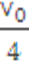
27.导体棒从开始到返回底端的过程中回路中产生的电能E。
28.导体棒在底端开始运动时的加速度的大小a。
正确答案
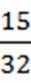
解析
根据能量守恒得
考查方向
能量守恒定律
解题思路
根据能量的转化与守恒,导体棒减少的动能转化为回路中的电能;
易错点
理解导体棒向上滑动过程中,克服安培力做功,把导体棒的动能转化为回路中的电能.
正确答案
5gsinθ(9分)
解析
在底端,设棒上电流为I,加速度为a,由牛顿第二定律,则:(mgsinθ+BIL)=ma
由欧姆定律,得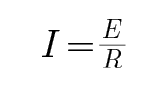
由上述三式,得
棒到达底端前已经做匀速运动则有:
代人数据,得a=5gsinθ
考查方向
牛顿第二定律
解题思路
导体棒在底端开始运动时受到重力、斜面的支持力和安培力的作用,沿斜面的方向重力的分力与安培力提供加速度,根据牛顿第二定律即可求出加速度.
易错点
关键抓住棒达到达底端前已做匀速运动,列出平衡方程找到此时安培力与重力沿导轨向下分量的关系.
扫码查看完整答案与解析