求函数y＝Asin(ωx＋φ)的解析式
共155题

· 求函数y＝Asin(ωx＋φ)的解析式

求函数y＝Asin(ωx＋φ)的解析式
共155题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

18.如图，在棱长为2的正方体ABCD-中，E，F分别是,的中点，

（1）证明：EF//.

（2）证明：三线共点.

（3）问：线段CD上是否存在一点G，使得直线FG与平面所成角的正弦值为，若存在，请指出点G的位置，说明理由；若没有，也请说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 14 分

21．如图，相距200海里的A、B两地分别有救援A船和B船。在接到求救信息后，A船能立即出发，B船因港口原因需2小时后才能出发，两船的航速都是30海里/小时．在同时收到求救信息后，A船早于B船到达的区域称为A区，否则称为B区。若在A地北偏东方向，距A地海里处的点有一艘遇险船正以10海里/小时的速度向正北方向漂移。

（1）求A区与B区边界线（即A、B两船能同时到达的点的轨迹）方程；

（2）问：①应派哪艘船前往救援？②救援船最快需多长时间才能与遇险船相遇？（精确到小时）

正确答案

（1）设点为边界线上的点，

由题意知，即，

即动点到两定点、的距离之差为常数，

∴点的轨迹是双曲线中的一支。

由得，

∴方程为（）

（2）①点的坐标为，点的坐标为，点的坐标为，

∴，，，

∴点在A区，又遇险船向正北方向漂移，

即遇险船始终在A区内，

∴应派A船前往救援

②设经小时后，A救援船在点处与遇险船相遇。

在中，，

∴

整理得，

解得或（舍）

∴A救援船需小时后才能与遇险船相遇

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 4 分

15．设x=sinα，且α∈，则arccosx的取值范围是（）

A[0， π]

B[，]

C[0，]

D[，π]

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

填空题 · 4 分

2．函数的定义域___________ 。

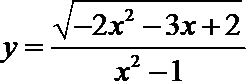
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

填空题 · 5 分

12．设是定义在上且周期为2的函数,在区间上,其中.若,则的值为____________。

正确答案

−10

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

继续学习学习下一知识点

下一知识点 : 函数y＝Asin(ωx＋φ)的应用

百度题库 > 高考 > 理科数学 > 求函数y＝Asin(ωx＋φ)的解析式

扫码查看完整答案与解析