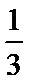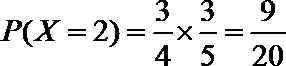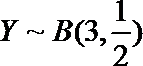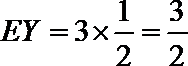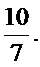- 二项分布与n次独立重复试验的模型
- 共5题
13.已知随机变量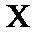
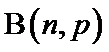
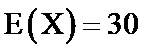
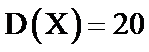
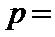
正确答案
解析
依题可得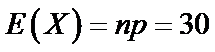
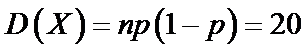
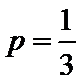
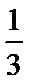
考查方向
解题思路
根据期望与方差的公式列出关于n,p的二元一次方程组,直接解出n,p。
易错点
二项分布的期望与方差的公式要分清楚,不要搞混了。
知识点
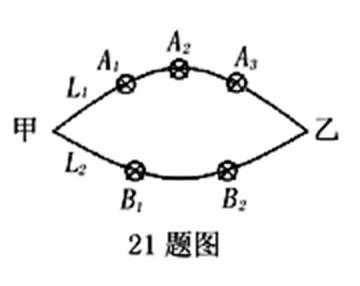
18.如图所示,张先生开车从甲地到乙地有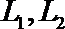
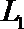
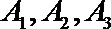

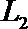
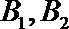
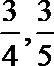
(Ⅰ)若走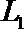
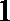
(Ⅱ)若走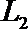
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
正确答案
解:
(Ⅰ)设走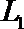
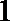
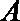
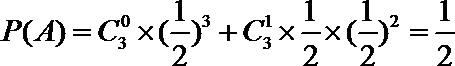
(Ⅱ)依题意,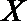
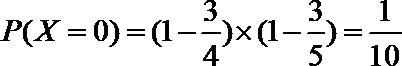
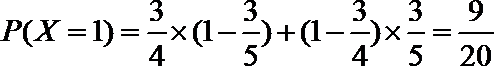
所以随机变量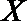
所以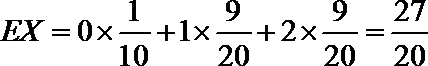
(Ⅲ)设选择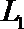
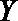
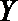
所以
因为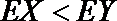
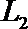

解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
袋中装有大小相同的黑球和白球共9个,从中任取2个都是白球的概率为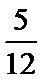
32.求袋中原有白球的个数;
33.求随机变量X的概率分布及数学期望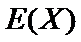
正确答案
详见解析
解析
(1)设袋中原有个白球,则从9个球中任取2个球都是白球的概率为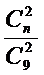
由题意知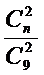
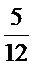
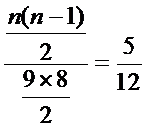
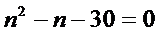
解得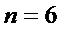
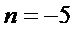
考查方向
离散型随机变量的期望与方差;等可能事件的概率;离散型随机变量及其分布列
解题思路
由题意知本题是一个等可能事件的概率的应用问题,试验发生包含的所有事件是从9个球中取2个球,共有C29种结果,而满足条件的事件是从n个球中取2个,共有Cn2种结果,列出概率使它等于已知,解关于n的方程,舍去不合题意的结果
易错点
考虑问题不全面,分类讨论有重漏
正确答案
详见解析
解析
(2)由题意,X的可能取值为1,2,3,4.
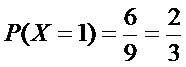
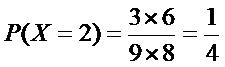
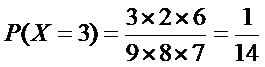
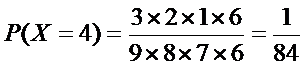
所以取球次数X的概率分布列为:

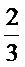
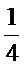
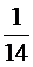
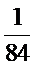
考查方向
离散型随机变量的期望与方差;等可能事件的概率;离散型随机变量及其分布列
解题思路
用X表示取球终止时取球的总次数,由题意知X的可能取值为1,2,3,4,结合变量对应的事件,用等可能事件的概率公式做出结果,写出分布列和期望
易错点
考虑问题不全面,分类讨论有重漏
15.已知随机变量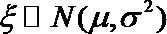
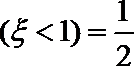
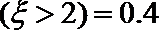
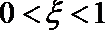
正确答案
0.1
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析