- 用其它方法求轨迹方程
- 共7题
已知点











23.当点



24.过点











正确答案
(1)
解析
(Ⅰ)设点





由

由



则由




考查方向
解题思路
1)第一问利用向量垂直的充要条件,以及


2)第二问首先设出





易错点
计算量大,未知数比较多,计算上出错。
正确答案
(2)
解析
(Ⅱ)由题意知直线


联立


∴





∴
∴
∴
∵

∴


考查方向
解题思路
1)第一问利用向量垂直的充要条件,以及


2)第二问首先设出





易错点
计算量大,未知数比较多,计算上出错。
15.在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别是AC1、A1B1的中点.点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知








正确答案
6
解析
根据角平分线定理,有


知识点
已知数列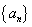
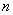
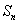
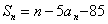
(1)证明: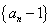
(2)求数列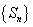
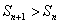

正确答案
见解析。
解析
知识点
15. 如图,直线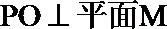

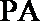
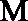
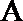
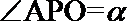
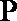
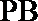

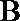
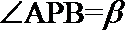
①若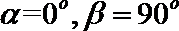
②若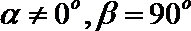
③若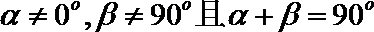
④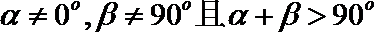
⑤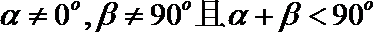
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析