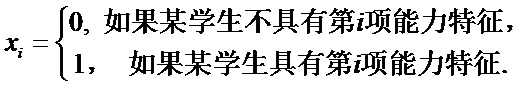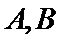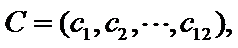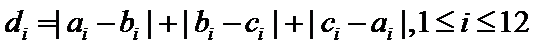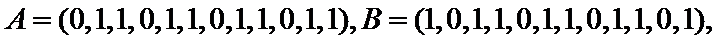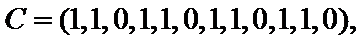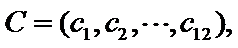- 排列、组合的实际应用
- 共39题
1
题型:填空题
|
10.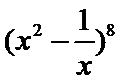
正确答案
-56
知识点
排列、组合的实际应用
1
题型:
单选题
|
如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为
正确答案
B
知识点
排列、组合的实际应用排列、组合及简单计数问题
1
题型:填空题
|
11.

正确答案
解析





考查方向
二项式定理.
解题思路
先求出二项式展开式的通项公式,再令X的次数等于2,求得r的值,即可得到展开式中的系数。
易错点
二项式展开错误,计算能力弱
知识点
排列、组合的实际应用
1
题型:填空题
|
14.某班主任在其工作手册中,对该班每个学生用十二项能力特征加以描述.每名学生的第
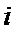
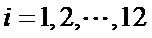
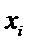
若学生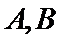
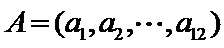
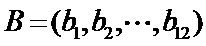
两名学生的不同能力特征项数为 (用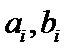
同学不同能力特征项数不少于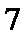
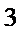
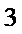
正确答案
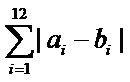
解析
设第三个学生为
因为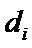
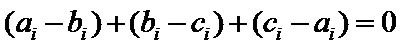
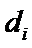
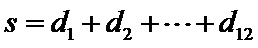
又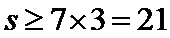
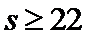
取
则不同能力特征项数总和恰为22 ,所以最小值为22 .
考查方向
本题主要考查了考生分析问题解决问题的能力,逻辑推理能力及数据处理能力,较难。
解题思路
理解清题意即可得到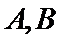
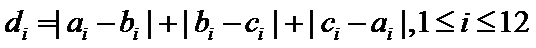
易错点
本题不易读懂题意,特别是对“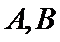
知识点
排列、组合的实际应用排列与组合的综合
下一知识点 : 排列、组合及简单计数问题
扫码查看完整答案与解析