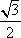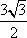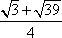- 解三角形的实际应用
- 共47题
1
题型:
单选题
|
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点










正确答案
C
解析
由勾股定理知,





则



所以


故

知识点
正弦定理解三角形的实际应用
1
题型:
单选题
|
在△ABC中,AC=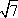
正确答案
B
解析
设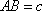
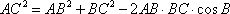
即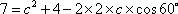
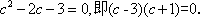
设BC边上的高等于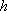
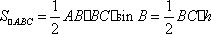
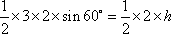
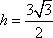
知识点
正弦定理余弦定理三角形中的几何计算解三角形的实际应用
1
题型:简答题
|
已知函数
(1)求函数
(2)在



求

正确答案
(1)
解析
(1)∵
∴
由

∴函数

(2)∵在

∴

又
∴
依据正弦定理,有
∴
∴
知识点
正弦函数的单调性三角函数中的恒等变换应用解三角形的实际应用
1
题型:
单选题
|
设△ABC的内角A, B, C所对的边分别为a, b, c, 若
正确答案
A
解析
因为
又

所以
知识点
解三角形的实际应用
1
题型:简答题
|
如图,游客从某旅游景区的景点


到




位游客从








速度为




(1)求索道
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在

乙步行的速度应控制在什么范围内?
正确答案
见解析
解析
(1)如图作BD⊥CA于点D,
设BD=20k,则DC=25k,AD=48k,
AB=52k,由AC=63k=1260m,
知:AB=52k=1040m。
知识点
任意角的三角函数的定义解三角形的实际应用
下一知识点 : 三角函数的最值
扫码查看完整答案与解析