- 等差数列的性质及应用
- 共237题
已知公差不为0的等差数列


(1)求数列
(2)设




正确答案
(1)
解析
解析:(1)设
由



联立①②得
故
(2)∵
∴
由
令

知识点
已知各项均为证书的数列





(1)求数列
(2)若


正确答案
(1)
解析
解析:(1)由题意知
当

当

两式相减得

∴数列


(2)由

所以,
所以数列


知识点
已知数列





正确答案
解析
知识点
已知点A(0,-1)在椭圆G:

(1)求椭圆G的方程;
(2)以CD为直径的圆恒过B点,求实数m的值。
正确答案
(1)
解析
(1)
所以椭圆G的方程是 
(2)因为直线CD与y轴不垂直,所以可设直线CD的方程为

设
判别式
CD为直径的圆恒过B(2,0)点,





知识点
已知数列





且公差

(1)求数列
(2)若

正确答案
见解析
解析
(1) 由
相减得:

∵当

∴数列
(2)∵
由题意
设

∴


故
知识点
已知等差数列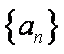
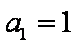
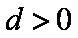
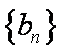
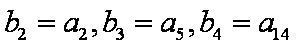
(1)求数列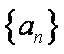
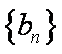
(2)设数列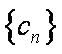
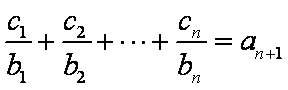
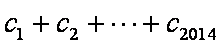
正确答案
见解析。
解析
(1)∵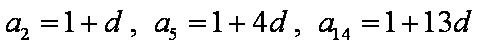
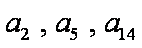
∴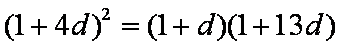
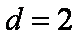
∴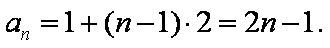
又∵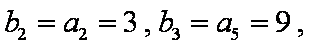
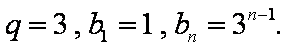
(2)∵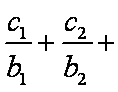
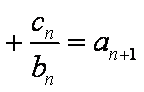
∴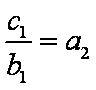
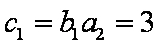
又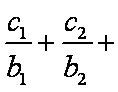
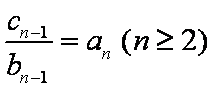
①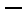
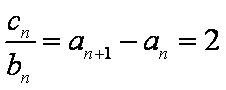
∴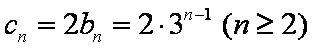
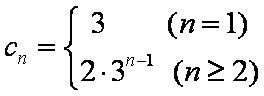
则
知识点
记数列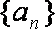
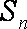
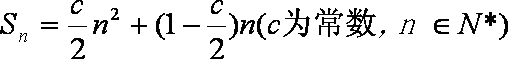
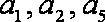
(1)求c的值;
(2)设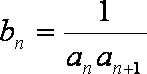
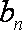
正确答案
见解析
解析
(1)由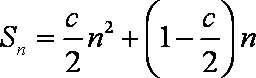
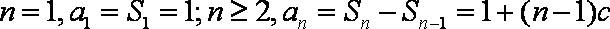
故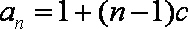
而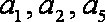
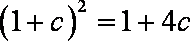
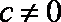
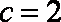
(2)由(1)知,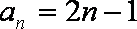
∴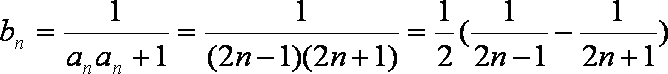
∴

知识点
17.在等比数列{an}中,a2=3,a5=81.
(1) 求an;
(2) 设bn=log3an,求数列{bn}的前n项和Sn。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在等差数列







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.等差数列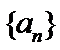
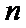
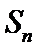
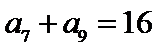
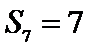
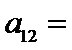
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析