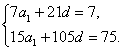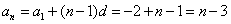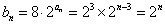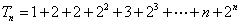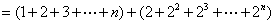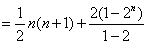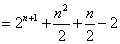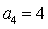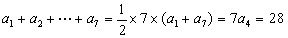- 等差数列的性质及应用
- 共237题
已知公差不为0的等差数列


(1)求数列
(2)对


正确答案
(1)

解析
(1)解:设等差数列{an}的公差为d,由
得
因为
故通项公式
(2)解:记

所以,当a>0时,
知识点
设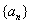
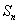
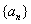
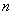
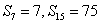
(1)求数列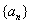
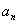
(2)设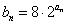
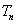
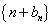
正确答案
见解析。
解析
(1)设等差数列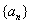
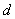
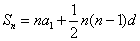
∵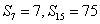
∴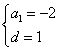
∴
(2)由(1)得
∴
知识点
在等差数列{an}中,已知a4+a8=16,则a2+a10=( )
正确答案
解析
由等差数列的性质知,a2+a10=a4+a8=16,故选B
知识点
已知等比数列{an}为递增数列,若a1>0,且2(an+an+2)=5an+1,则数列{an}的公比q=__________。
正确答案
2
解析
∵等比数列{an}为递增数列,且a1>0,
∴公比q>1。
又∵2(an+an+2)=5an+1,
∴2an+2anq2=5anq。
∵an≠0,∴2q2-5q+2=0。
∴q=2或
∴公比q为2
知识点
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;
p2:数列{nan}是递增数列;
p3:数列
p4:数列{an+3nd}是递增数列。
其中的真命题为( )。
正确答案
解析
如数列-2,-1,0,1,2,…,则1×a1=2×a2,排除p2,如数列1,2,3,…,则
知识点
已知等差数列{an}的前n项和Sn满足S3=0,S5=-5.
(1)求{an}的通项公式;
(2)求数列
正确答案
(1)an=2-n.
(2)
解析
(1)设{an}的公差为d,则Sn=
由已知可得
解得a1=1,d=-1.
故{an}的通项公式为an=2-n.
(2)由(1)知

从而数列
=
知识点
如果等差数列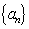
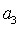
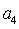
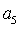
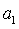
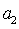
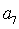
正确答案
解析
∵ 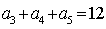
知识点
已知等差数列{

正确答案
解析
略
知识点
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列。
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|。
正确答案
(1)an=-n+11,n∈N*或an=4n+6,n∈N*
(2)
解析
(1)由题意得5a3·a1=(2a2+2)2,
即d2-3d-4=0.
故d=-1或d=4.
所以an=-n+11,n∈N*或an=4n+6,n∈N*.
(2)设数列{an}的前n项和为Sn,因为d<0,由(1)得d=-1,an=-n+11.则当n≤11时,|a1|+|a2|+|a3|+…+|an|=Sn=
当n≥12时,|a1|+|a2|+|a3|+…+|an|=-Sn+2S11=
综上所述,|a1|+|a2|+|a3|+…+|an|=
知识点
已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列。
(1)求{an}的通项公式;
(2)求a1+a4+a7+…+a3n-2.
正确答案
(1)an=-2n+27.
(2)Sn=-3n2+28n.
解析
(1)设{an}的公差为d.
由题意,
即(a1+10d)2=a1(a1+12d)。
于是d(2a1+25d)=0.
又a1=25,所以d=0(舍去),d=-2.
故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.
由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列。
从而Sn=

知识点
扫码查看完整答案与解析