等差数列的性质及应用
共237题

· 等差数列的性质及应用

等差数列的性质及应用
共237题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 12 分

等差数列{}中，

（I）求{}的通项公式；

(II)设=[]，求数列{}的前10项和，其中[x]表示不超过x的最大整数，如[0.9]=0,[2.6]=2.

正确答案

(Ⅰ)设数列的公差为d。由题意有，解得，

所以的通项公式为.

（Ⅱ）由(Ⅰ)知，

当n=1,2,3时，；

当n=4,5时，；

当n=6,7,8时，；

当n=9,10时，，

所以数列的前10项和为.

知识点

等差数列的性质及应用其它方法求和数列与不等式的综合数列与其它知识的综合问题

题型：简答题

简答题 · 12 分

已知是公差为3的等差数列,数列满足,.

17.求的通项公式；

18.求的前n项和.

第(1)小题正确答案及相关解析

正确答案

解析

：

考查方向

等差数列与等比数列

解题思路

易错点

将等差、等比数列中的五个基本量转化成方程应用题，注意运算.

第(2)小题正确答案及相关解析

正确答案

解析

（II）由（I）和 ,得,因此是首项为1,公比为的等比数列.记的前项和为,则

考查方向

等差数列与等比数列

解题思路

易错点

将等差、等比数列中的五个基本量转化成方程应用题，注意运算.

题型：填空题

填空题 · 5 分

8.已知{an}是等差数列，Sn是其前n项和.若a1+a22=3，S5=10，则a9的值是 .

正确答案

知识点

等差数列的性质及应用

题型：填空题

填空题 · 5 分

4.已知一组数据4.7,4.8,5.1,5.4,5.5，则该组数据的方差是______________.

正确答案

0.1

知识点

等差数列的性质及应用

题型：填空题

填空题 · 4 分

14.无穷数列{an}由k个不同的数组成，Sn为{an}的前n项和.若对任意的，则k的最大值为 .

正确答案

知识点

等差数列的性质及应用

题型：填空题

填空题 · 12 分

已知数列{an}的首项为1， Sn为数列{an}的前n项和，Sn+1=qSn+1，其中q﹥0，n∈N+

(Ⅰ)若a2，a3，a2+a3成等差数列，求数列{an}的通项公式；

(Ⅱ)设双曲线x2﹣=1的离心率为en，且e2=2，求e12+ e22+…+en2，

正确答案

（本小题满分12分）

（Ⅰ）由已知，两式相减得到.

又由得到，故对所有都成立.

所以，数列是首项为1，公比为q的等比数列.

从而.

由成等差数列，可得，所以，故.

所以.

（Ⅱ）由（Ⅰ）可知，.

所以双曲线的离心率.

由解得.所以，

，

知识点

等差数列的性质及应用数列与解析几何的综合

题型：简答题

简答题 · 12 分

17.

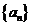
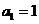
已知各项都为正数的数列满足，.

（I）求；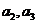

（II）求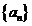的通项公式.

正确答案

（Ⅰ）由题意得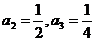. .........5分

（Ⅱ）由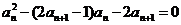得.

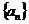
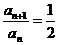
因为的各项都为正数，所以.

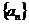
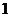
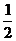
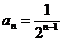
故是首项为，公比为学.科网的等比数列，因此. ......12分

知识点

等差数列的性质及应用

题型：简答题

简答题 · 12 分

17. 已知是公差为3的等差数列，数列满足，.

（I）求的通项公式；

（II）求的前n项和.

正确答案

解：(1) ∵ anbn+1+bn+1=nbn ∴ n=1时 a1·b2+b2=b1

∴ a1·+=1 ∴ a1=2 由已知{an}乘以2为首项，公差3的等差数列

∴ an=a1+(n-1)·d=2+3(n-1) ∴ an=3n-1

(2)由①知an=3n-1代入an·bn+1+bn+1=nbn中

∴ (3n-1)bn+1+bn+1=nbn ∴ bn+1=bn (n∈n*)

∴ 设{bn}构成以1为首项，公比为的等比数列

∴ 设{bn}前n项和Sn，则

知识点

等差数列的性质及应用

题型：简答题

简答题 · 16 分

本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分.

对于无穷数列{}与{}，记A={|=，}，B={|=，}，若同时满足条件：①{}，{}均单调递增；②且，则称{}与{}是无穷互补数列.

25.若=，=，判断{}与{}是否为无穷互补数列，并说明理由；

26.若=且{}与{}是无穷互补数列，求数列{}的前16项的和；

27.若{}与{}是无穷互补数列，{}为等差数列且=36，求{}与{}的通项公式.

第(1)小题正确答案及相关解析

正确答案

与不是无穷互补数列

解析

因为，，所以，

从而与不是无穷互补数列．

考查方向

数列通项、求和、综合应用；

解题思路

用特殊值验证，得出不满足互补

易错点

理解题意

第(2)小题正确答案及相关解析

正确答案

180

解析

因为，所以．

数列的前项的和为

．

考查方向

数列通项、求和、综合应用；

解题思路

数列求和

易错点

计算

第(3)小题正确答案及相关解析

正确答案

，

解析

解：

设的公差为，，则．

由，得或．

若，则，，与“与是无穷互补数列”矛盾；

若，则，，．

综上，，．

考查方向

数列通项、求和、综合应用；

解题思路

设出等差数列的通项公式，推理论证.

易错点

公式的掌握和具体计算

题型：填空题

填空题 · 5 分

8.已知是等差数列，是其前项和．若，，则的值是．

正确答案

；

解析

设公差为，则由题意可得，，

解得，，则．

考查方向

等差数列定义通项以及前n项和。

解题思路

根据等差数列的通项以及求和列出方程组，求出基本量然后求特定项。

易错点

列方程求基本量致误

知识点

等差数列的性质及应用

继续学习学习下一知识点

下一知识点 : 等差数列的前n项和及其最值

百度题库 > 高考 > 文科数学 > 等差数列的性质及应用

扫码查看完整答案与解析