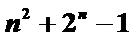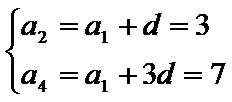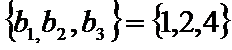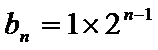- 等差数列的性质及应用
- 共237题
18. 已知数列


(Ⅰ)求

(Ⅱ)设



正确答案
(1)


解析
试题分析:本题属于等差数列及数列的求和,
(1)直接利用公式来解答;
(2)先利用裂项相消法求出
(Ⅰ)设数列


由

所以

(Ⅱ)可得

由于

即

考查方向
解题思路
本题考查等差数列及数列的求和,解题步骤如下:(1)直接利用公式来解答;(2)先利用裂项相消法求出
易错点
第二问求和不晓得使用裂项相消法去做。
知识点
10. 数列




正确答案
解析
设数列

所以

考查方向
解题思路
先求出公差d,再根据等差数列的性质求出a11
易错点
对等差数列的性质运用错误
知识点
已知等差数列



18. 求
19. 设



正确答案
见解析
解析
(Ⅰ)设等差数列



解得
考查方向
解题思路
根据

易错点
主要易错于公比q=1的判断,
正确答案
见解析
解析
(Ⅱ)






考查方向
解题思路
利用等比数列的判定得到数列是等比数列
易错点
主要易错于公比q=1的判断,
14.已知{

正确答案
-1
解析
考查方向
解题思路
1)使用等差数列通项公式使用a1和d表示
2)使用等比中项公式得到关系式
易错点
主要易错于计算出错
知识点
17.已知数列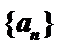
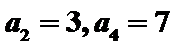
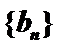
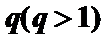
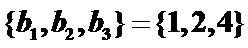
(Ⅰ)求数列

(Ⅱ)求数列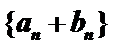
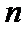
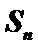
正确答案
(1)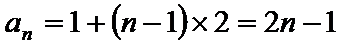
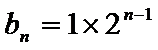
解析
试题分析:本题属于数列中的基本问题,题目的难度不大,(1)直接按照步骤来求(2)利用求和公式来解.
(Ⅰ)设等差数列的首项和公差分别为: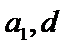
解得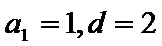

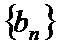
∴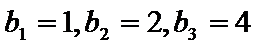
∴
(Ⅱ)
=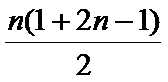
= 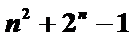
考查方向
解题思路
本题考查等差数列和等比数列以及数列的求和,解题步骤如下:
用待定系数法构造关于首项和公差公比的方程组。
等差等比的求和公式。
易错点
第2问不知道分组求和。
知识点
扫码查看完整答案与解析