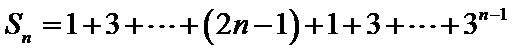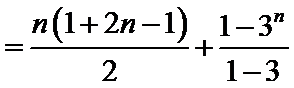- 等差数列的性质及应用
- 共237题
1
题型:简答题
|
已知{an}是等差数列,{bn}是等差数列,且b2=3,b3=9,a1=b1,a14=b4.
15.求{an}的通项公式;
16.设cn=an+bn,求数列{cn}的前n项和.
第(1)小题正确答案及相关解析
正确答案
(I)等比数列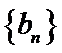
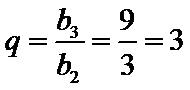
所以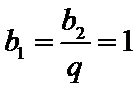
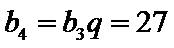
设等差数列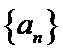
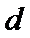
因为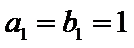
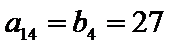
所以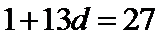
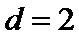
所以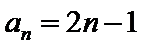
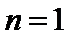
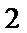
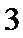
考查方向
等差数列 等比数列的通项公式和求和公式的应用
解题思路
(1)利用数列的公式,列方程,解方程
(2)利用数列求和公式进行计算
易错点
分清等差数列与等比数列,应用相应公式计算
第(2)小题正确答案及相关解析
正确答案
由(I)知,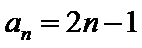
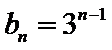
因此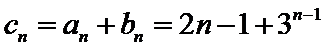
从而数列
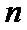
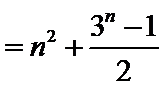
考查方向
等差数列 等比数列的通项公式和求和公式的应用
解题思路
(1)利用数列的公式,列方程,解方程
(2)利用数列求和公式进行计算
易错点
分清等差数列与等比数列,应用相应公式计算
1
题型:
单选题
|
3.设




正确答案
C
解析
由
又
考查方向
等差数列的

解题思路
由
结合
易错点

教师点评
综合考查数列求和公式和性质的应用
知识点
等差数列的基本运算等差数列的性质及应用
1
题型:简答题
|
已知等差数列









23.求数列

24.记

第(1)小题正确答案及相关解析
正确答案
解析
(1)由





从而

在已知
当





考查方向
考查等差数列与等比数列通项公式,以及给出数列的递推公式,求通项公式的方法
解题思路
先解一元二次方程可得


易错点
熟悉已知递推关系求数列通项公式的方法
第(2)小题正确答案及相关解析
正确答案


考查方向
考查比较大小的方法,求差比较法
解题思路
求出数列
易错点
熟悉求差比较法
下一知识点 : 等差数列的前n项和及其最值
扫码查看完整答案与解析