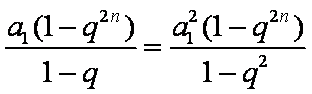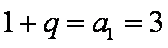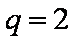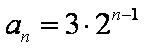- 等差数列的性质及应用
- 共237题
在右图的算法中,最后输出的a,b的值依次是 .
正确答案
2,1
解析
第四步c变为1,第五步a变为2,第五步b变为1
知识点
若




正确答案
13
解析
方法一:


方法二: 
方法三:由



知识点
在等比数列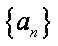
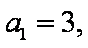
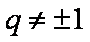
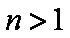
(1)求数列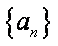
(2)若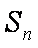
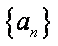
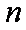
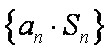
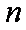
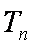
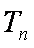
正确答案
见解析。
解析
因为数列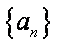
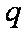
所以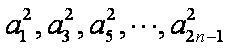
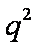
故
而
所以
整理得
所以
所以
(2) 数列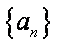
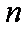
所以
故
因为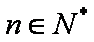
所以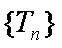
所以当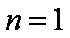
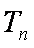
求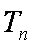
令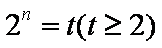
此时二次函数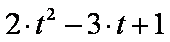
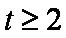
故当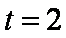
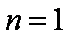
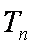
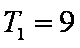
知识点
设数列






(1)求数列
(2)当m=1时,求
(3)设





正确答案
见解析。
解析
(1)由已知




所以数列





②-①得
所以

(3)
因为


注意到,当n为奇数时,


所以


对于任意的正整数n都有
所以
知识点
已知等差数列
正确答案
15
解析

知识点
对于任意的



①


(1)数列







(2)若各项为正数的等比数列






(3)数列







正确答案
见解析
解析
解析:(1)在数列




在数列












(2)由于数列

代入



所以


对于任意的

所以数列


(3)由于


由于任意



即

即






即


满则条件②只需

所以
知识点
设数列







(1)当


(2)当




正确答案
(1)


解析
解析:由题意知
两式相减得
即
(1)当
于是
又

故知,
再由

(2)当

若


若


若







所以,当

知识点
设数列{



数列{
(1)若数列{



(2)若数列{

正确答案
见解析
解析
解:(1)由题意,得




所以
(2)证明:由{








由{



















则


所以


于是


所以

知识点
设公差不为零的等差数列

(1)求数列
(2)试求所有的正整数m,使得

正确答案
见解析。
解析
(1)因为



设


化简得



但若



于是
(2)因为

所以要使


于是

但由于


由



当



所以所求m的值为3和4。
另解:因为

所以要使


于是

知识点
已知公差不为0的等差数列


(1)求数列
(2)设




正确答案
见解析。
解析
(1)设
由




故
(2)∵
∴
由
令

知识点
扫码查看完整答案与解析