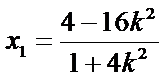- 圆锥曲线的综合问题
- 共211题
21.已知椭圆





(1)求椭圆
(2)若动直线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
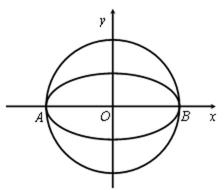
20.如图,椭圆



(Ⅰ)求椭圆
(Ⅱ)直线







正确答案
(Ⅰ)
(Ⅱ)不存在直线
解析
(Ⅰ)因为椭圆



又离心率为


所以


(Ⅱ)设直线AP的方程为
因为圆心到直线

所以
因为
将直线与椭圆方程联立:
得到
因为已知有一根为-4,所以另一根为
代入得到

显然


考查方向
解题思路
将比例进行转化:
易错点
第二问不能把比例进行转化,而试图去求PQ的长度,却无法求出来。
知识点
21.在平面直角坐标系



(1)求椭圆C的方程;
(2)设椭圆C的上下顶点分别为



(3)在椭圆C上,是否存在点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知抛物线





(1)求证:


(2)设


正确答案
解:(1)设直线的方程为:
联立方程可得

设





而

即


(2)由


即得:

由(1)中②代入得

解析
解析已在路上飞奔,马上就到!
知识点
20.设椭圆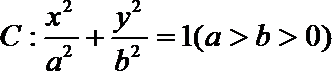
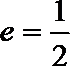
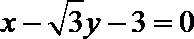
(I)求椭圆C的方程;
(II)在(I)的条件下,过右焦点F2作斜率为k的直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.在平面直角坐标系



(1)求椭圆C的方程;
(2)设椭圆C的上下顶点分别为



(3)在椭圆C上,是否存在点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,椭圆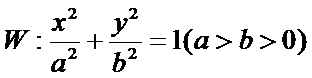
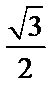
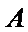
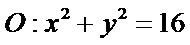
(Ⅰ)求椭圆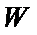
(Ⅱ)直线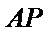
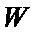
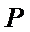

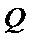
(i)当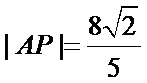
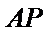
(ii)是否存在直线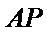
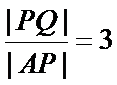
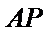
说明理由.
正确答案
(Ⅰ)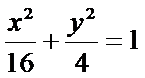
(Ⅱ)(i)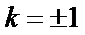
(ii)不存在直线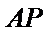
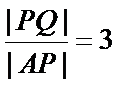
解析
(Ⅰ)
因为椭圆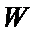

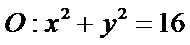
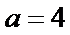
又离心率为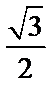
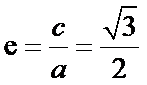
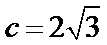
所以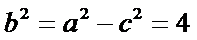
所以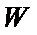
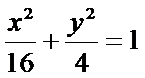
(Ⅱ)(i)
法一:设点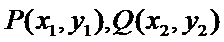
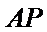
设直线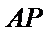
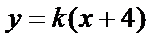
与椭圆方程联立得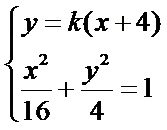
化简得到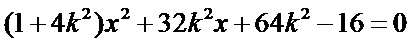
因为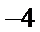

所以
由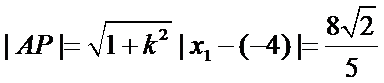
代入得到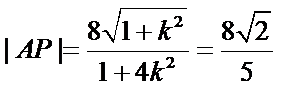
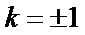
所以直线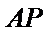
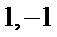
(ii)因为圆心到直线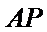
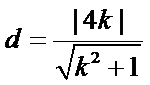
所以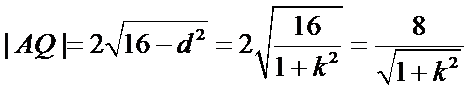
因为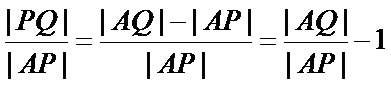
代入得到
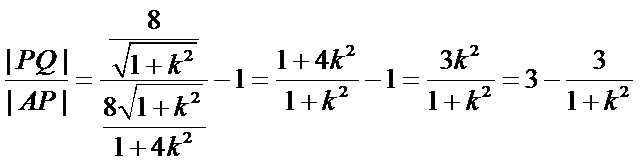
显然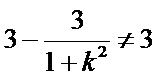
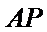
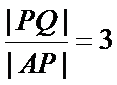
法二:(i)设点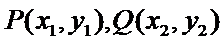
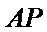
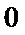
设直线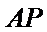
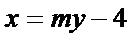
与椭圆方程联立得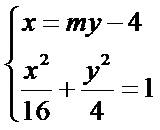
化简得到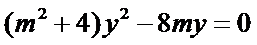
显然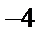
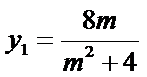
由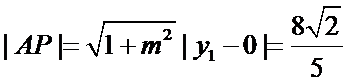
代入得到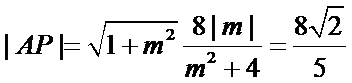
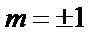
所以直线
(ii)因为圆心到直线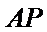
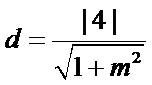
所以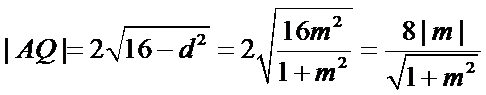
因为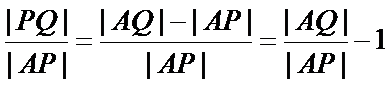
代入得到
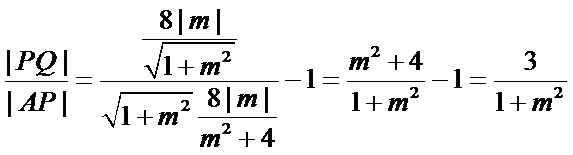
若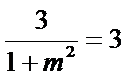
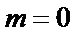
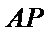
所以不存在直线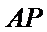
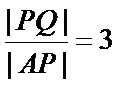
考查方向
本题考查了椭圆的综合求解能力,在近几年的各省高考题出现的频率较高.
解题思路
(Ⅰ)由椭圆的左顶点求出a,再有离心率求出c,进而求得b的值;
(Ⅱ)(i)联立方程,利用韦达定理求得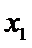
(ii)利用垂径定理求解.
易错点
计算量大,易出错.
知识点
20. 椭圆









(Ⅰ)求椭圆

(Ⅱ)设














正确答案
(Ⅰ)



解析
题 是解析几何中的常规题,两个椭圆的组合给学生解题带来很大的心理压力,只要能突破这一障碍,总体来讲难度还是不大的。
(Ⅰ)依题意




由对称性,四个焦点构成的四边形为菱形,且面积
解得:
所以椭圆


(Ⅱ)(1)设



所以:



(2)设



所以:
同理:



结合(1)有
考查方向
考查了椭圆方程的求法,以及椭圆中的定值问题,对学生的运算和思维能力要求较高。两个椭圆组合起来,显得条件较多,对学生的解题形成很大的干扰。
解题思路
本题考查椭圆的性质及运用,解题步骤如下:1、设出椭圆的方程,由两个条件得出两个方程,解方程组。2、设动点求斜率之积为常数;
易错点
1、不能正确的设出两个椭圆的方程,
2、(2)(3)问中运算量较大,可能出错。
知识点
20. 椭圆C的对称中心是原点,对称轴是坐标轴,离心率与双曲线

(1)求出椭圆方程;
(2)一条纵截距为2的直线l1与椭圆C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程;
(3)直线l2:

正确答案
(1)
(2)
(3)不存在直线
解析
试题分析:本题直线与圆锥曲线的综合应用问题,解析如下:
解: (1)双曲线
所以椭圆的离心率为
设椭圆的长半轴为

半焦距为
所以
所以
设椭圆的方程为

所以
所以椭圆的标准方程为
(2)直线

设直线为

得:
由



以

①即
也即
即
将①式代入,得
即
解得
所以
(3)由方程组
得
设
则
所以
因为直线
所以

则

考查方向
本题考查了求椭圆的标准方程,直线与圆锥曲线的位置关系等知识点,属于拔高题。
易错点
利用已知条件整理容易出错。
知识点
20. 如图,在平面直角坐标系














(1)求椭圆
(2)若点








(3)是否存在点


正确答案
(1) 
(2)
(3)存在点

解析
试题分析:本题属于解析几何的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意计算的准确性,
(1)由



所以椭圆









所以椭圆
(2)将




由点




联立直线


又





所以点


故
(3)假设存在点


当直线


当直线


由


所以若存在点


根据对称性,只需考虑直线



又设直线


化简得


又
所以
将上述关系代入,化简可得
综上所述,存在点

考查方向
本题主要考查了本题考查了椭圆的集合性质和直线与椭圆的位置关系
解题思路
(1)因直线





(2)将

求出点B到直线PA的距离h;
(3)假设存在点E,使得
易错点
(1)计算的准确性
(2)存在性问题,先特殊在一般
知识点
扫码查看完整答案与解析