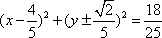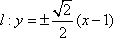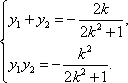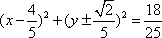圆锥曲线的综合问题_章节学习

1

题型：简答题

|

简答题 · 13 分

已知椭圆的离心率为，直线与以原点为圆心，

椭圆的短半轴为半径的圆相切。

（1）求椭圆的方程；

（2）设椭圆与曲线的交点为、，求面积的最大值。

正确答案

见解析

解析

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

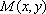
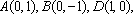
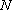
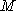
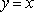
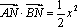
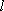
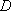
在平面直角坐标系中，已知动点，点点与点关于直线对称，且.直线是过点的任意一条直线。

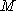
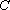
（1）求动点所在曲线的轨迹方程；

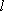
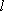
（2）设直线与曲线交于两点，且，求直线的方程；

（3）设直线与曲线交于两点，求以的长为直径且经过坐标原点的圆的方程。

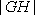
正确答案

（1）（2）（3）

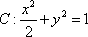
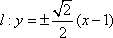
解析

（1）依据题意，可得点.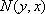

，

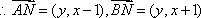
又，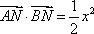

.

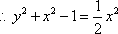
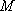
所求动点的轨迹方程为.

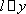
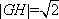
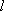
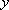
（2）若直线轴，则可求得，这与已知矛盾，因此满足题意的直线不平行于轴。

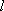
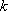
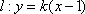
设直线的斜率为，则。

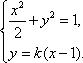
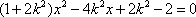
由得。

设点，有且恒成立（因点在椭圆内部）。

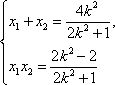
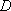
又，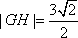

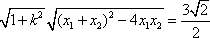
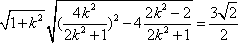
于是，，即，

解得。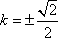

所以，所求直线

（3）当直线轴时，，点到圆心的距离为1.即点在圆外，不满足题意.

满足题意的直线的斜率存在，设为，则.

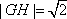
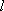
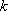
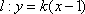
设点，由（2）知，进一步可求得

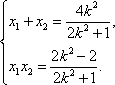
依据题意，有，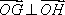

，

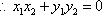
即，解得.

所求圆的半径，

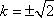
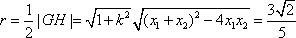
圆心为.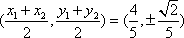

所求圆的方程为：

知识点

直线的一般式方程直线与圆锥曲线的综合问题直接法求轨迹方程直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

已知双曲线的离心率为2，一个焦点与抛物线的焦点相同，则双曲

线的渐近线方程为

A

B

C

D

正确答案

A

解析

略

知识点

直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 14 分

已知椭圆（）的焦点坐标为，离心率为，直线交椭圆于，两点。

（1）求椭圆的方程；

（2）是否存在实数，使得以为直径的圆过点？若存在，求出的值；若不存在，请说明理由。

正确答案

（1）

（2）

解析

（1）由，，得，，

所以椭圆方程是： ……………………4分

（2）设，则，

将代入，整理得（*）

则 ………………………7分

以PQ为直径的圆过，则，即

， ………………………………12分

解得，此时（*）方程，

所以存在，使得以为直径的圆过点， ……14分

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

如图，已知椭圆：的离心率为，以椭圆的左顶点为圆心作圆：，设圆与椭圆交于点与点。

（1）求椭圆的方程；

（2）求的最小值，并求此时圆的方程；

（3）设点是椭圆上异于,的任意一点，且直线分别与轴交于点，为坐标原点，求证：为定值，

正确答案

见解析。

解析

（1）

故椭圆的方程为，

（2）点与点关于轴对称，设，，不妨设。

由于点在椭圆上，所以，（*）

由已知，则，，

。

由于，故当时，取得最小值为。

由（*）式，，故，又点在圆上，代入圆的方程得到，

故圆的方程为：，

（3）

知识点

向量在几何中的应用圆的标准方程椭圆的定义及标准方程直线与圆锥曲线的综合问题直线、圆及圆锥曲线的交汇问题

1

题型：填空题

|

填空题 · 5 分

以抛物y2＝4x的焦点为圆心且与双曲线的渐近线相切的圆的方程

是＿＿＿＿

正确答案

解析

略

知识点

圆的标准方程椭圆的几何性质抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

已知抛物线的焦点为椭圆的右焦点,且椭圆的长轴长为4，M、N是椭圆上的的动点。

（1）求椭圆标准方程；

（2）设动点满足：，直线与的斜率之积为，证明：存在定点，使得为定值，并求出的坐标；

（3）若在第一象限，且点关于原点对称，垂直于轴于点，连接并延长交椭圆于点，记直线的斜率分别为，证明：。

正确答案

见解析。

解析

（1）由题设可知：因为抛物线的焦点为，

所以椭圆中的又由椭圆的长轴为4得

故

故椭圆的标准方程为：

（2）设，

由可得：

由直线OM与ON的斜率之积为可得：

，即

由①②可得：

M、N是椭圆上的点，故

故，即

由椭圆定义可知存在两个定点，

使得动点P到两定点距离和为定值;

（3）设，由题设可知

，

由题设可知斜率存在且满足.③

将③代入④可得：

⑤

点在椭圆，

故

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 14 分

已知抛物线和双曲线都经过点,它们在x轴上有共同焦点，对称轴是坐标轴，抛物线的定点为坐标原点。.

（1）求抛物线和双曲线标准方程；

（2）已知动直线m过点P(3,0),交抛物线于A，B两点，记以线段AP为直径的圆为圆C，

求证：存在垂直于x轴的直线l被圆C截得的弦长为定值，并求出直线l的方程。

正确答案

见解析。

解析

知识点

双曲线的定义及标准方程抛物线的标准方程和几何性质直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题直线、圆及圆锥曲线的交汇问题

1

题型：单选题

|

单选题 · 5 分

已知焦点在轴的椭圆方程为，过椭圆长轴的两顶点做圆的切线，若切线围成的四边形的面积为，则椭圆的离心率为

A

B

C

D

正确答案

A

解析

略

知识点

椭圆的几何性质直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 16 分

已知椭圆C：的离心率，一条准线方程为。

（1）求椭圆C的方程；

（2）设G，H为椭圆上的两个动点，O为坐标原点，且OG⊥OH。

①当直线OG的倾斜角为60°时，求△GOH的面积；

②是否存在以原点O为圆心的定圆，使得该定圆始终与直线GH相切？若存在，请求出该定圆方程；若不存在，请说明理由。

正确答案

见解析。

解析

（1）因为椭圆的离心率，一条准线方程为。

所以，，a2=b2+c2，

解得，

所以椭圆方程为，

（2）①由，解得，

由得，

所以，所以，

②假设存在满足条件的定圆，设圆的半径为R，则OG•OH=R•GH

因为OG2+OH2=GH2，故，

当OG与OH的斜率均存在时，不妨设直线OG方程为：y=kx，与椭圆方程联立，可得，

∴

同理可得

∴，∴R=

当OG与OH的斜率有一个不存在时，可得

故满足条件的定圆方程为x2+y2=。

知识点

椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点