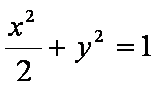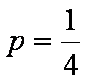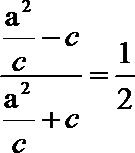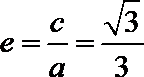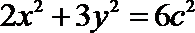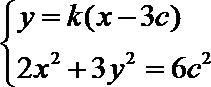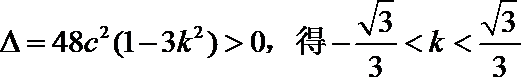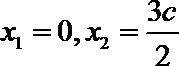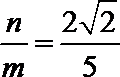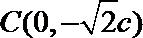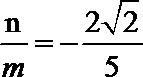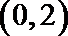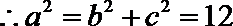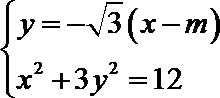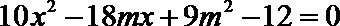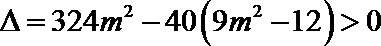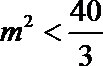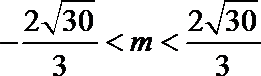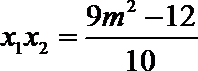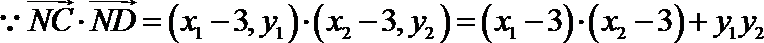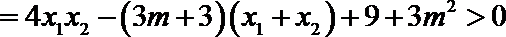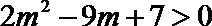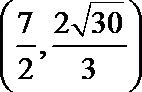- 圆锥曲线的综合问题
- 共211题
如图,焦距为2的椭圆D的两个顶点分别为



(1)求椭圆D的标准方程;
(2)过点

正确答案
(1)
(2)
解析
(1)设椭圆E的标准方程为






∴

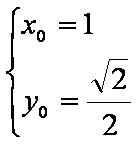
(2)设


消去y,得,
∴



∵以PQ为直径的圆经过原点O ∴

又
由


∴
知识点
已知椭圆
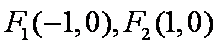


(1)求椭圆
(2)若抛物线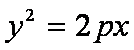
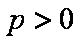

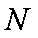
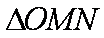
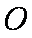
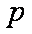
正确答案
见解析
解析
(1)依题意,设椭圆

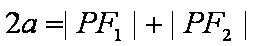
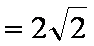
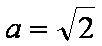
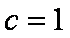
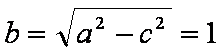

(2)根据椭圆和抛物线的对称性,设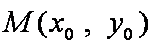
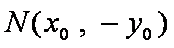
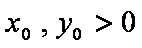
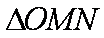
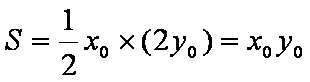
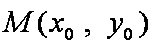
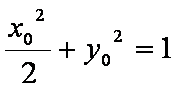
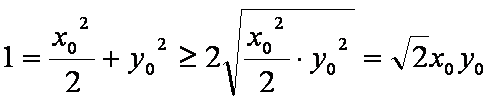
当且仅当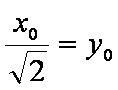
解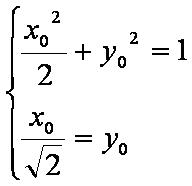
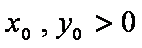

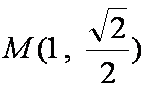
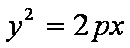
所以
知识点
已知双曲线







正确答案
解析
略
知识点
11.以抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 过双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆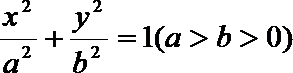
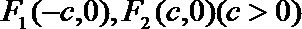
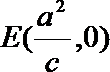
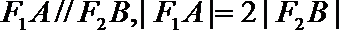
(1)求椭圆的离心率; 求直线
(2)设点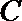
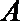
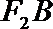
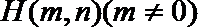
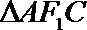

正确答案
解:(1)由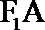
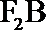
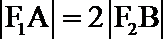
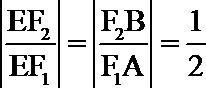
整理,得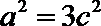
由(1)得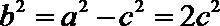
设直线AB的方程为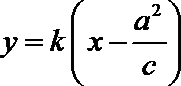
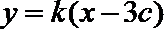
由已知设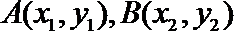
消去y整理,得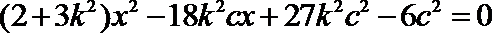
依题意,
而 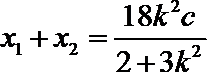
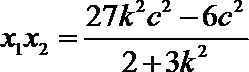
由题设知,点B为线段AE的中点,所以
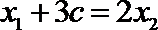
联立①③解得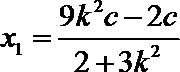
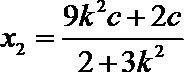
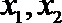
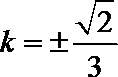
(2)解法一:可知
当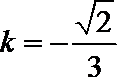
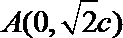
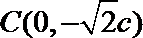
线段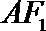
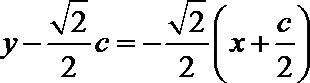
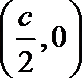
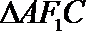
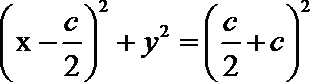
直线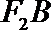
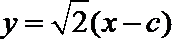
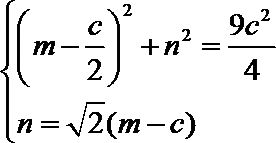
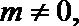
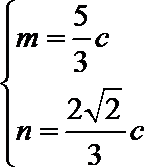
当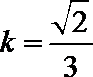
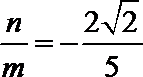
解法二:可知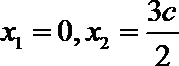
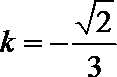
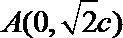
由椭圆的对称性可知B,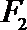
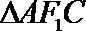
且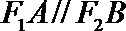
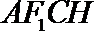
由直线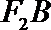
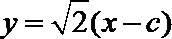
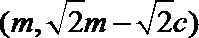
因为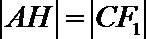
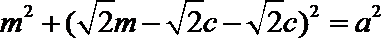
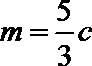
则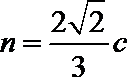
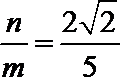
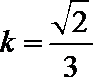
解析
解析已在路上飞奔,马上就到!
知识点
14.已知圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知圆
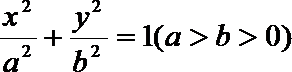
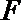

(1)求椭圆的方程;
(2)过椭圆外一点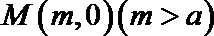

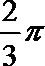
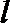
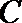
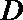
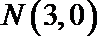
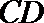
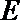
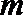
正确答案
(1)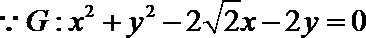
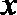
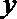
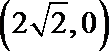
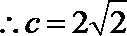

(2)设直线
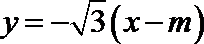
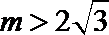
可得:
可得:
即
设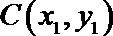

则
化简得:
可得: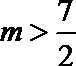
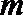
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,抛物线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析