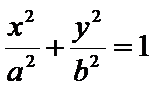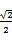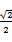- 圆锥曲线的综合问题
- 共211题
5. 





正确答案
解析
由抛物线方程可知,准线方程为x=-










考查方向
解题思路
首先求抛物线的准线方程,再由抛物线的定义,过A,B向准线作垂线段, 再设A,B两点到y轴的距离为





易错点
抛物线的性质, 数学结合的应用.
知识点
已知






24.求该椭圆的离心率;
25.设

正确答案
.e=
解析
当线段A


因为cos∠







考查方向
解题思路
先证出

易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
正确答案


解析
由24得椭圆方程为




则直线AC的方程为y=






(2) 若AB⊥x轴,则



综上所述,

考查方向
解题思路
由24得到含有b的椭圆方程,根据题意对直线AB、AC的斜率进行分为讨论,设出坐标,联立方程组,利用根与系数关系,结合向量关系式,将向量关系转化为坐标关系,用A的坐标及b,表求

易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
11. 已知双曲线





正确答案
解析
如图,易知A(





考查方向
解题思路
画出简图,得出A(



易错点
不能利用双曲线的性质找到a,b,c系的关系
知识点
10.已知双曲线

正确答案
解析
抛物线

所以,

故此题答案为
考查方向
解题思路
先根据题意抛物线的焦点坐标为(2,0)从而得出

易错点
本题较简单,只要抛物线的定义及双曲线渐近线方程等知识熟知就不会出错。
知识点
11. 已知双曲线





正确答案
解析
如图,易知A(





考查方向
解题思路
画出简图,得出A(



易错点
不能利用双曲线的性质找到a,b,c系的关系
知识点
11. 已知双曲线





正确答案
解析
如图,易知A(





考查方向
解题思路
画出简图,得出A(



易错点
不能利用双曲线的性质找到a,b,c系的关系
知识点
5. 





正确答案
解析
由抛物线方程可知,准线方程为x=-










考查方向
解题思路
首先求抛物线的准线方程,再由抛物线的定义,过A,B向准线作垂线段, 再设A,B两点到y轴的距离为





易错点
抛物线的性质, 数学结合的应用.
知识点
已知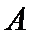
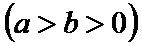
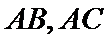
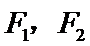
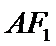
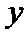
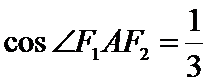
24.求该椭圆的离心率;
25.设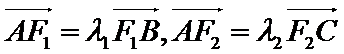
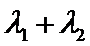
正确答案
.e=
解析
当线段A
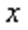
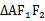
因为cos∠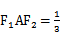
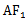
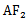
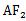

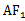

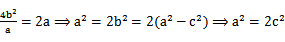
考查方向
解题思路
先证出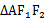
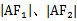
易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
正确答案
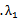

解析
由24得椭圆方程为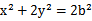

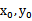

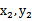
则直线AC的方程为y=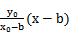
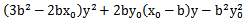
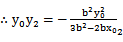


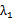
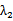
(2) 若AB⊥x轴,则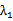
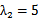
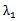
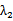
综上所述,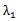
考查方向
解题思路
由24得到含有b的椭圆方程,根据题意对直线AB、AC的斜率进行分为讨论,设出坐标,联立方程组,利用根与系数关系,结合向量关系式,将向量关系转化为坐标关系,用A的坐标及b,表求
易错点
解析几何易出现对于直线方程的分类讨论上的错,其次就是直线与曲线联系以后,寻求向量、坐标、常数、参数之间的联系时,易出现转化和计算、代数整理上的错误。
8. 若圆


正确答案
解析
只需求圆心(0,1)到曲线


距离
所以,若圆与曲线无公共点,则0< r<
故选C。
考查方向
解题思路
先根据题意取曲线上的点


易错点
本题易在理解题意上出现错误。本题易在用变量得到距离后求最值时极易出错。
知识点
7.在平面直角坐标系中,双曲线




正确答案
解析
已知双曲线的渐近线方程为

把点



A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
已知双曲线的渐近线方程

把所给点代入上面方程,即得
易错点
双曲线的焦点位置不好确定,不会设双曲线方程的形式。
知识点
扫码查看完整答案与解析