- 圆锥曲线的综合问题
- 共211题
已知椭圆

(1)求椭圆C的方程;
(2)过椭圆C上的动点P引圆O:x2+y2=b2的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所
引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在, 请说明理由。
正确答案
见解析。
解析
(1)设椭圆的半焦距为c,依题意
∴b=2,
∴所求椭圆方程为
(2)如图,设P点坐标为(x0,y0),
若∠APB=900,则有
即
有
两边平方得
又因为P(x0,y0)在椭圆上,所以
①,②联立解得
所以满足条件的有以下四组解



所以,椭圆C上存在四个点



知识点
已知椭圆






(1)求椭圆的方程;
(2)是否存在实数



正确答案
(1)
(2)
解析
(1)由




所以椭圆方程是:
(2)设


将


则
以PQ为直径的圆过


解得

所以 存在


知识点
已知双曲线




正确答案
解析
略
知识点
某海域有











(1)求曲线
(2)某日,研究人员在







正确答案
(1)


解析
解析:(1)由题意知曲线


又


所以曲线

(2)由于


因此设此时距


即鱼群分别距

设









知识点
已知椭圆C:


(1)求椭圆C的方程;
(2)设G,H为椭圆上的两个动点,O为坐标原点,且OG⊥OH。
①当直线OG的倾斜角为60°时,求△GOH的面积;
②是否存在以原点O为圆心的定圆,使得该定圆始终与直线GH相切?若存在,请求出该定圆方程;若不存在,请说明理由。
正确答案
见解析。
解析
(1)因为椭圆的离心率

所以

解得
所以椭圆方程为
(2)①由

由

所以

②假设存在满足条件的定圆,设圆的半径为R,则OG•OH=R•GH
因为OG2+OH2=GH2,故
当OG与OH的斜率均存在时,不妨设直线OG方程为:y=kx,与椭圆方程联立,可得
∴
同理可得
∴
当OG与OH的斜率有一个不存在时,可得
故满足条件的定圆方程为x2+y2=
知识点
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”。
如图,“盾圆






(1)求椭圆的方程;
(2)是否存在过







正确答案
见解析
解析
(1)由


又


(2) 设直线

联立


联立


8分


整理得
若



同理

知识点
已知直角坐标平面内一动点


(1)求动点

(2)过点






(3)过点






正确答案
见解析
解析
(1)由抛物线的定义,知所求P点的轨迹是以




所以,动点P的轨迹C的方程为
(2)由题意知,直线AB的方程为
代入

设



又


即

因此

综上,实数

(3)设过点






于是


又

设存在直线

化简,得
所以,

所以


所以,当


知识点
已知椭圆





(1)求椭圆
(2)若动直线








正确答案
见解析
解析
由

椭圆C的标准方程为









又Q








知识点
20.已知椭圆



(Ⅰ)求椭圆
(Ⅱ)若直线









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,设点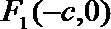
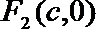
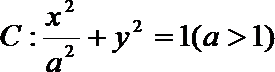
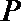
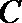

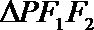
(1)求椭圆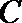
(2)设直线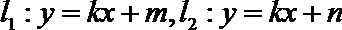
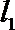
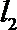
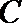
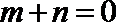
(3)在(2)的条件下,试探究在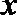
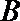

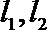
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析