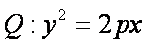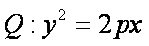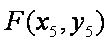- 不等式的性质
- 共307题
已知抛物线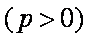
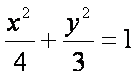
(1)求抛物线Q的方程;
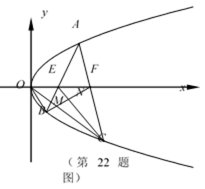
(2)如图所示,设A、B、C是抛物线Q上任意不同的三点,且点A位于x轴上方,B、C位于x轴下方. 直线AB、AC与x轴分别交于点E、F,BF与直线OC、EC分别交于点M、N. 记△OBM、△ENF、△MNC的面积依次为S1、S2、S3,求证:S1+S2=S3.
正确答案
见解析
解析
解:(1)∵椭圆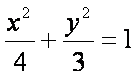
由于抛物线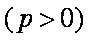
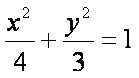
∴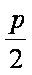
(2) 设点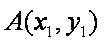
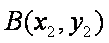
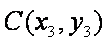
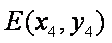
由题,要证S1+S2=S3,即证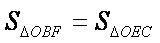
即证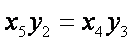
设直线AB的方程为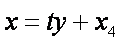
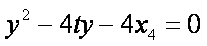
由韦达定理得,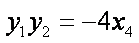
同理可得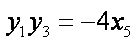
①×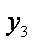
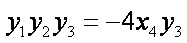
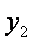
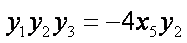
∴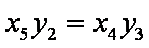
知识点
(不等式选讲)已知函数

正确答案
解析
由






知识点
11.设x,y满足约束条件,则z=x+2y的最大值为( )
正确答案
解析
作出不等式对应的平面区域,由z=x+2y,得y=﹣



由

故选B.
知识点
3.设x、y是两个实数,命题“x、y中至少有一个数大于1”成立的充分不必要条件是( )
正确答案
解析
若
所以
所以x+y>2是x、y中至少有一个数大于1成立的充分不必要条件.
故选B
知识点
若
正确答案
解析
因为



知识点
设
(1)当

(2)当



正确答案
见解析
解析
(1)-

所以解集为
(2)当

令
由图像知:当


由题意知:


知识点
若x,y满足约束条件
正确答案
-3
解析
画出线性约束条件


知识点
(若不等式|kx-4|≤2的解集为{x|1≤x≤3},则实数k= 。
正确答案
2
解析
由




知识点
15.若不等式

正确答案
解析
由于





知识点
7.已知x,y满足约束条件
正确答案
解析
由约束条件
联立
B(3,0),
化目标函数z=2x+y为y=﹣2x+z,
由图可知,当直线y=﹣2x+z过A时,直线在y轴上的截距最小,z最小等于2×1﹣1=1;
当直线y=﹣2x+z过B时,直线在y轴上的截距最大,z最大等于2×3﹣0=6.
∴a+b=1+6=7.
故选:A.
知识点
扫码查看完整答案与解析