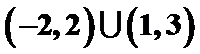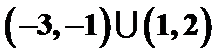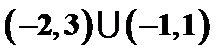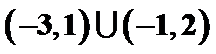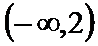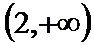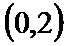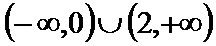- 不等式的性质
- 共307题
11.对于问题:“已知关于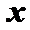
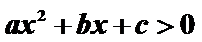
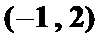
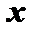
等式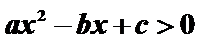
解:由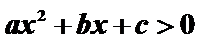
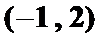
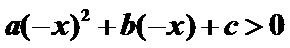
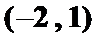
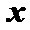
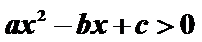
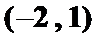
参考上述解法,若关于
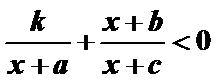
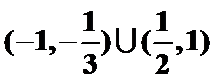
则关于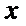
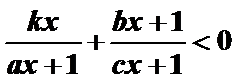
正确答案
解析
找到对应的关系,即只要将原来的x换成
考查方向
解题思路
先根据前面已知的不等式找到规律再求解所求不等式即可。
易错点
本题不知道怎样转化。
知识点
已知函数f(x)=-2lnx+x2-2ax+a2,其中a>0.
27.设g(x)为f(x)的导函数,讨论g(x)的单调性;
28.证明:存在a∈(0,1),使得f(x)≥g(x).
正确答案
当x∈(0,1)时,g'(x)<0,g(x)单调递减
当x∈(1,+∞)时,g'(x)>),g(x)单调递增;
解析
由已知,函数f(x)的定义域为(0,+∞)
g(x)=f '(x)=2(x-1-lnx-a)
所以g'(x)=2-
当x∈(0,1)时,g'(x)<0,g(x)单调递减
当x∈(1,+∞)时,g'(x)>),g(x)单调递增
考查方向
解题思路
1.第(1)问直接利用单调区间的求法求解即可;
易错点
第(1)问注意不到定义域导致出错;
正确答案
证明详见解析
解析
由f '(x)=2(x-1-lnx-a)=0,解得a=x-1-lnx
令Φ(x)=-2xlnx+x2-2x(x-1-lnx)+(x-1-lnx)2=(1+lnx)2-2xlnx
则Φ(1)=1>0,Φ(e)=2(2-e)<0
于是存在x0∈(1,e),使得Φ(x0)=0
令a0=x0-1-lnx0=u(x0),其中u(x)=x-1-lnx(x≥1)
由u'(x)=1-
故0=u(1)<a0=u(x0)<u(e)=e-2<1
即a0∈(0,1)
当a=a0时,有f '(x0)=0,f(x0)=Φ(x0)=0
再由(I)知,f '(x)在区间(1,+∞)上单调递增
当x∈(1,x0)
当x∈(x0,+∞)时,f '(x)>0,从而f(x)>f(x0)=0
又当x∈(0,1]时,f(x)=(x-a0)2-2xlnx>
故x∈(0,+∞)时,f(x)≥0
综上所述,存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.
考查方向
解题思路
.第(2)问先构造函数Φ(x)=-2xlnx+x2-2x(x-1-lnx)+(x-1-lnx)2=(1+lnx)2-2xlnx,后得到函数u(x)=x-1-lnx(x≥1),然后即可证明结论。
易错点
第(2)问根本不知道该如何构造函数导致没有思路。
已知函数
24.当

25.当

26.若对于任意的


正确答案
(Ⅰ)当


解析
(Ⅰ)当




当



当



∴当


考查方向
解题思路
直接求导,判断导数的正负后即可得到极值;
易错点
无
正确答案
(Ⅱ)当



当


当



解析
(Ⅱ)当




由



(1)当




(2)当


(3)当



在
综上所述,
当



当


当



考查方向
解题思路
求导后分类讨论导数的正负后确定函数的单调区间;
易错点
在求函数的单调性时,不会确定分类的标准;
正确答案
(Ⅲ)
解析
(Ⅲ)由(Ⅱ)知,当


∴
∵对于任意的

∴

∴

当


∴实数

考查方向
解题思路
先根据第(2)问放缩后构造不等式
易错点
不会放缩
10. 若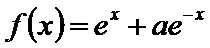
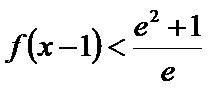
正确答案
解析
若f(x)=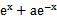
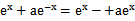
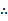
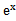
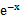
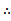
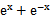
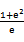
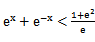
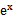
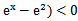
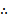
考查方向
解题思路
先由偶函数性质,求出a=1,将不等式进行化简整理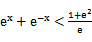
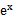
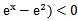
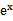
易错点
不等式的化简整理
知识点
肺炎患者神昏谵语,舌謇肢厥。其证型是
A.邪热内闭
B.热陷心包
C.邪热伤阴
D.邪热伤阳
E.阴竭阳脱
正确答案
B
解析
暂无解析
3. 若
正确答案
解析
所以选C
考查方向
对数值的大小的比较
解题思路
分别利用指数式与对数函数的运算性质比较三个数与0和1的大小得答案
易错点
对数的相关性质混淆
知识点
9.已知函数f(x)=x2+bx+c且f(1+x)=f(-x),则下列不等式中成立的是( )
正确答案
解析
可知函数图象开口向上,对称轴是x=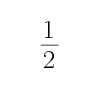
考查方向
本题考查二次函数的单调性和对称性。
解题思路
先确定二次函数的对称轴,在根据图象开口方向及单调性确定大小。
易错点
方向出错,对称轴无法确定,等。
教师点评
本题考查了二次函数的性质,在近几年的各省高考题出现的频率较高,常与抽象函数等知识点交汇命题。
知识点
扫码查看完整答案与解析