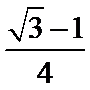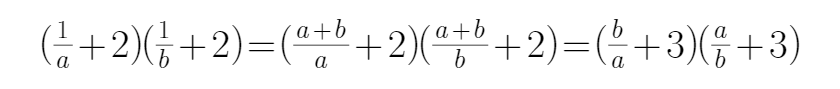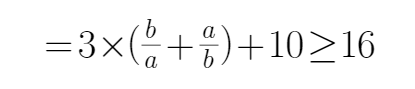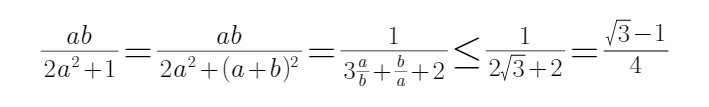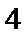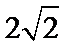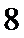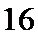- 基本不等式及不等式的应用
- 共144题
15.已知正数x,y满足
正确答案
3
解析
考查方向
解题思路
1)令2x+y=t→y=t-2x带入计算
2)化简可以得到
易错点
主要易错于均值定理的构建过程
知识点
14.已知正数


正确答案
9
解析


考查方向
解题思路
本题考查基本不等式的求最值应用,解题步骤如下:将要求的表达式乘以x+y然后化简后利用基本不等式即可解出。
易错点
本题不会将1用x+y代入求解。
知识点
13.已知a>0,b>0,且a+b=1,求
正确答案
4
解析

考查方向
解题思路
先变形,换成基本不等式的形式
易错点
不等式的性质应用时,等价转换错误
知识点
15.已知正数


正确答案
10
解析


考查方向
解题思路
本题考查基本不等式的求最值应用,解题步骤如下:将要求的表达式乘以x+y然后化简后利用基本不等式即可解出。
易错点
本题不会将9用x+y代入求解。。
知识点
12.已知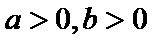
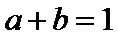
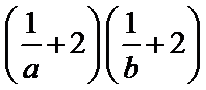
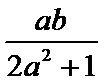
正确答案
16;
解析
考查方向
平均值不等式的性质和运算
解题思路
根据平均值不等式的性质结合题木求出最大值和最小值
易错点
计算化简错误
知识点
6.已知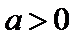
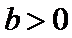
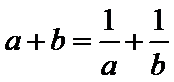
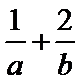
正确答案
解析
由已知可知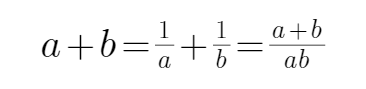
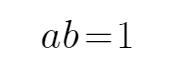
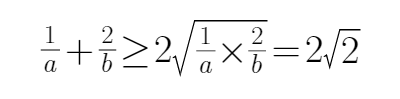
考查方向
平均值不等式的性质
解题思路
利用均值不等式求最小值
易错点
找不到“一正、二定、三相等”条件
知识点
某企业生产一种产品,单价8元,单位变动成本6元,固定成本2 000元,预计产销量为2 000件,若想实现利润3 000元,可采取的措施有( )。
A.固定成本降低1000
B.单价提高到8.5元
C.单位变动成本降低到5.5元
D.销量捉高到2500件
E.单价降低到7元,销量提高到2500件
正确答案
A,B,C,D
解析
[解析] 利润=销售数量×单价-销售数量×单位变动成本-固定成本总额3 000=2 000×8-2 000×6-固定成本总额,固定成本总额=1 000(元)3000=2 000×单价-2 000×6-2 000,单价=8.5(元)3 000=2 000×8-2 000×单位变动成本-2 000,单位变动成本=5.5(元)3 000=销售量×8-销售量×6-2 000,销售量=2500(件)2500×7-2500×6-2000=500元,所以选项E不正确。
12.如果函数

正确答案
18
解析



















考查方向
解题思路
本题考查运用函数的单调性解决不等式问题,解题步骤如下:分三种情况讨论。
详解见解析。
易错点
本题必须注意分类讨论,忽视则会出现错误。
知识点
正确答案
1
知识点
扫码查看完整答案与解析