- 基本不等式及不等式的应用
- 共144题
已知函数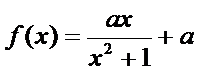

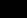
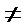
25.求函数f (x)的单调区间;
26.证明:当a > 0时,对于任意x1,x2∈(0,e],总有g(x1) < f (x2)成立,其中
正确答案
(1)当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1);
解析
(Ⅰ)函数f (x)的定义域为R,f ′(x)=
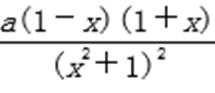
当a>0时,当x变化时,f ′(x),f(x)的变化情况如下表:
当a<0时,当x变化时,f ′(x),f(x)的变化情况如下表:
综上所述,
当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
考查方向
解题思路
1)第一问对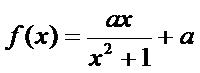
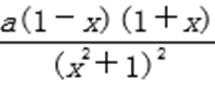
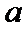
2)第二问由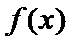
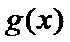
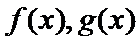
正确答案
(2)略;
解析
(Ⅱ)由(Ⅰ)可知,当a>0时,f (x)在区间(0,1)上单调递增,f (x)
f (x)在区间(1,e]上单调递减,且f (e)=
因为g(x)=aln x-x,所以g′(

①当a≥e时,g′(x)≥0在区间(0,e]上恒成立,
所以函数g(x)在区间(0,e]上单调递增,所以g(x)max=g(e)=a-e<a.
所以对于任意x1,x2∈(0,e],仍有g(x1)<f(x2).
②当0<a
因为a-(aln a-a)=a(2-ln a)>a(2-ln e)=a>0,
所以对任意x1,x2∈(0,e],总有g(x1)<f (x2).
综上所述,对于任意x1,x2∈(0,e],总有g(x1)<f (x2).
考查方向
解题思路
1)第一问对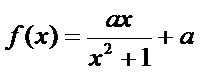
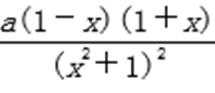

2)第二问由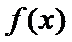
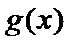
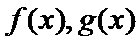
10. 若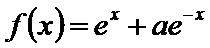
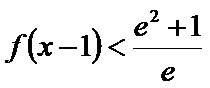
正确答案
解析
若f(x)=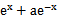
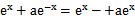
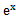
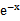
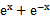
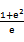
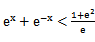
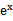
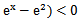
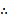
考查方向
解题思路
先由偶函数性质,求出a=1,将不等式进行化简整理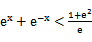
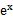
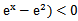
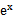
易错点
不等式的化简整理
知识点
10. 若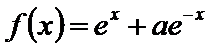
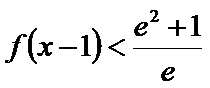
正确答案
解析
若f(x)=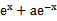
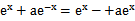
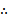
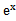
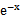
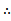
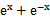
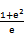
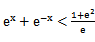
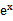
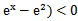
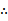
考查方向
解题思路
先由偶函数性质,求出a=1,将不等式进行化简整理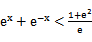
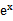
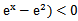
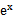
易错点
不等式的化简整理
知识点
世博中学为了落实上海市教委推出的“阳光运动一小时”活动,计划在一块直角三角形









(1)试用


(2)设矩形









正确答案
(1)

解析
解析:(1)在

所以
矩形


于是
(2) 矩形

又

即草坪造价
由总造价
所以


当且仅当

此时


所以选取

知识点
如图,在
(1)当棱锥
(2)若点P为AB的中点,E为
正确答案
见解析
解析
(1)设
,则
令
则
由上表易知:当

证明:
(2)
作
由已知得:

所以
知识点
若对任意










(1)非负性:

(2)对称性:
(3)三角形不等式:
今给出四个二元函数:①



能够成为关于的

正确答案
①
解析
略
知识点
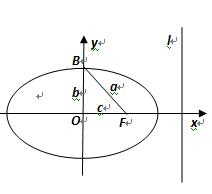
在平面直角坐标系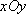
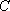
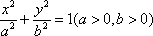
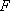
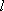
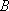
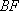
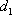
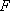
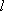
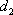
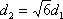
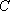
正确答案
解析
如图,l:x=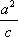
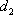
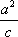
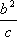
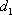
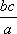
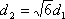
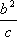
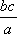
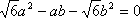
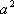
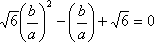

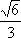
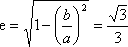
知识点
若实数


正确答案
解析
略
知识点
在如图所示的锐角三角形空地中, 欲建一个面积最大的内接矩形花园(阴影部分), 则其边长x为 () (m)。
正确答案
20
解析
利用均值不等式解决应用问题。设矩形高为y, 由三角形相似得:

知识点
设

正确答案
解析
略
知识点
扫码查看完整答案与解析