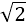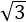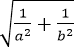- 基本不等式及不等式的应用
- 共144题
18.某建筑公司用8000万元购得一块空地,计划在该地块上建造一栋至少12层.每层4000平方米的楼房。经初步估计得知,如果将楼房建为x(x
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=
正确答案
解:设楼房每平方米的平均综合费为

法一:
当且仅当
因此,当

为了使楼房每平方米的平均综合费最少,该楼房应建为20层,每平方米的平均综合费最小值为5000元
法二:
解析
解析已在路上飞奔,马上就到!
知识点
9.设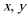
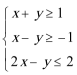
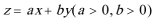
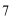
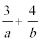
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设x,y均为正数,且
正确答案
49
解析


知识点
6.在四边形ABCD中,M为AC上一点,且




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知总体的各值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5。若要使该总体的方差最小,则a,b的取值分别是________
正确答案
10.5 10.5
解析
这10个数的中位数为
要使总体方差最小,即要(a-10)2+(b-10)2最小,即a2+b2-20(a+b)+200最小,
∵a>0,b>0,∴a2+b2≥
又a+b=21,∴当a=b=10.5时,方差取得最小值。
知识点
6.已知a=(x,1),b=(2,-x),那么
正确答案
解析



若x=0,则
若x>0,由于


则0<


若x<0,由于-

则




即-

知识点
4.若直线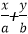
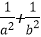
正确答案
解析
设向量m=(cosα,sinα),n=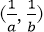
由题意知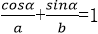
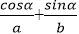
即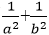
知识点
6.已知0<x<2,则
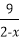
正确答案
解析
因为0<x<2,所以0<2-x<2,
所以
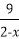

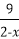
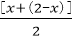
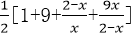
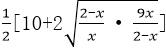
当且仅当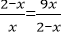

知识点
4.若数列满足

正确答案
解析
依题意可得bn+1=pbn,则数列为等比数列。又b1b2b3…b99=599,所以b50=5,故b10·b90=
知识点
扫码查看完整答案与解析