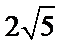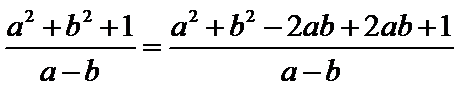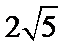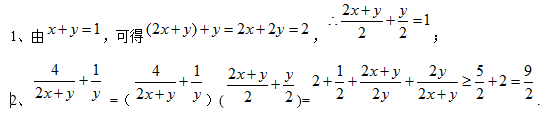- 基本不等式及不等式的应用
- 共144题
13.若2x+2y=1,则x+y的取值范围是 。
正确答案
(-∞,-2],
解析


考查方向
解题思路
本题考查采用基本不等式即可解出来。
易错点
本题考察了基本不等式,注意不等式的使用条件是一正二定三相等。
知识点
8.已知a+b(a>0,b>0)是函数

正确答案
解析
1、由题可知,易得a+b=30-3a,即4a+b=30。
考查方向
解题思路
本题考查函数的零点及基本不等式,解题步骤如下:利用基本不等式求解即可
易错点
本题易在应用基本不等式的公式时发生错误。
知识点
13. 已知实数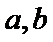
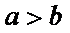
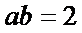
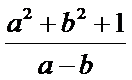
正确答案
解析
因为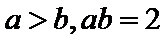
所以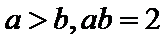
因为
所以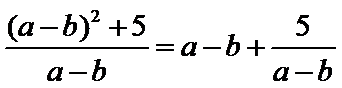
因为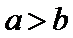
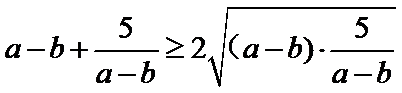
所以最小值为
考查方向
解题思路
先化简成基本不等式情况,然后再利用不等式性质求
易错点
想不到利用基本不等式,而是利用二次函数求最值
知识点
13.若2x+2y=1,则x+y的取值范围是 。
正确答案
(-∞,-2],
解析


考查方向
解题思路
本题考查采用基本不等式即可解出来。
易错点
本题考察了基本不等式,注意不等式的使用条件是一正二定三相等。
知识点
4.函数





正确答案
解析
定点A(1,-1)在直线
考查方向
本题主要考查函数过定点问题及最值问题
解题思路
求出定点A,得出m,n的关系m+n=1,再用乘1法
易错点
1、定点A求不出来;
2、最值求解的基本方法不熟悉。
知识点
4.已知直线


正确答案
解析
连续抛掷两颗骰子得到的基本事件总数是





考查方向
易错点
计算过程注意使用均值定理的条件
知识点
14.若

正确答案
解析
所以最小值是
考查方向
解题思路
1、对多项式展开得到

易错点
本题易错于使用双重不等式忽略等号成立条件
知识点
15.已知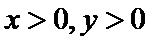
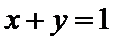
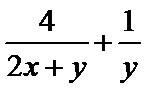
正确答案
解析
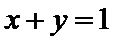
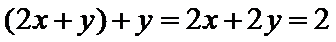
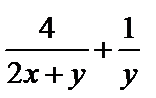
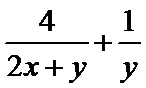
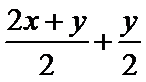
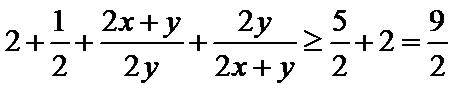
考查方向
本题主要考查了基本不等式求最值。
解题思路
易错点
知识点
6.设


正确答案
解析
根据题意知,


考查方向
本题主要考查了等比数列与均值不等式的综合应用,在近几年的各省高考题出现的频率较高,常与数列、不等式等知识点交汇命题。
易错点
均值不等式取等条件容易忽视。
知识点
14.己知平行四边形的周长为6,则其对角线长的平方和的最小值是 .
正确答案
9
解析
试题分析:本题属于平面向量和基本不等式的问题,题目的难度较小。注意转化为平面向量求解。
考查方向
本题主要考查了平面向量和基本不等式的问题。
解题思路
本题考查平面向量,解题步骤如下:
设平行四边形的两邻边分别为向量a,b,夹角为θ。则对角线的平方和为
(a+b)2+(a-b)2=2a2+2b2≥(a+b)2=9。
易错点
本题必须注意转化为平面向量的问题求解,忽视则会出现错误。
知识点
扫码查看完整答案与解析