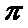- 直接法求轨迹方程
- 共25题
15.如图,在边长为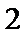
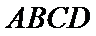
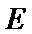
现将△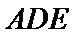
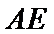
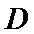
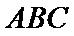

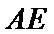
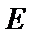
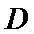
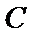
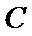
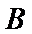
则点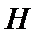
正确答案
解析
由题意,在平面AED内过点D作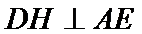
则
当E从点D运动到C,再从C运动到B,故H点的轨迹是以AD'为直径的半圆弧,
根据边长为2的正方形ABCD知圆半径是1,
所以其所对的弧长为π,
故答案为:π
考查方向
解题思路
根据图形的翻折过程中变与不变的量和位置关系知,在平面AED内过点D作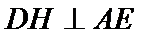
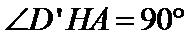
易错点
主要易错于信息的转化失败,导致计算出错
知识点
6.到两条互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )
正确答案
解析
在边长为a的正方体ABCD-A1B1C1D1中,DC与A1D1是两条互相垂直的异面直线
平面ABCD过直线DC且平行于A1D1,以D为原点
分别以DA,DC所在直线为x轴,y轴建立平面直角坐标系
设点P(x,y)在平面ABCD内,且到A1D1与DC的距离相等
则|x|=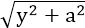
知识点
20.已知P为圆A:(x + l)2+y2=8上的动点,点B(1,0),线段PB的垂直平分线与半径PA相交于点M,记点M的轨迹为P.(1)求曲线P的方程;(2)当点P在第一象限,且COS∠BAP=
正确答案
1)圆A的圆心为A(-1,0),半径为
由已知得,
于是,
故曲线P是以A,B为焦点,
以
故曲线P的方程为
(2)由点P在第一象限,


于是直线AP方程为:
代入椭圆方程,消去y,可得,
所以,
由于点M在线段AP上,所以点M的坐标为
解析
已知圆心为A(-1,0),半径为

考查方向
本题主要考查直线和圆的方程的应用
解题思路
根据已知条件求出曲线的方程,根据曲线方程求出点的坐标。
易错点
椭圆的方程定义不清楚,计算能力弱
知识点
20.已知点M(-1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N距离的
(Ⅰ)求曲线E的方程;
(Ⅱ)已知m≠0,设直线l1:x-my-1=0交曲线E于A,C两点,直线l2:mx+y-m=0交曲线E于B,D两点.若CD的斜率为-1,求直线CD的方程.
正确答案
(1)
(2)y=-x,或y=-x+3.
解析
(1)直接按照步骤来求
(2)要注意对参数的讨论.
⑴解:设曲线

由题意,
整理得

⑵解:由题知

设曲线


线段



设直线

由

由圆的几何性质,





所以直线


考查方向
本题考查了圆的标准方程和直线与圆的位置关系,属于高考中的高频考点.
解题思路
解题步骤如下:
1、利用已知求解。
2、联立直线与圆方程求解。
易错点
第二问中表示直线斜率时容易出错。
知识点
19.已知曲线Γ上的点到



(1)求曲线Γ的方程;
(2)若

(3)设点





正确答案
(1)曲线Γ的方程为
(2)
(3)
解析
本题综合性较强,题目有一定难度,需要透彻理解抛物线的定义,巧设直线方程,灵活运用一元二次方程根与系数的关系来求。
解:(1)因为点到




(2)设A(x1,y1),B(x2,y2)因为直线过F(1,0),所以设lAB:x=my+1,又因为










考查方向
本题是一个综合性很强的题目,考查了抛物线的定义,直线的斜率、向量的坐标式、一元二次方程根与系数关系等知识,在抛物线、向量、方程根等处进行了交汇,有一点的难度,考查了学生对基础知识的掌握能力、综合运用能力。
易错点
第二问中设直线方程为x=my+1,可以使解题方便,若设y=k(x-1),需要考虑斜率不存在的情况.
知识点
扫码查看完整答案与解析