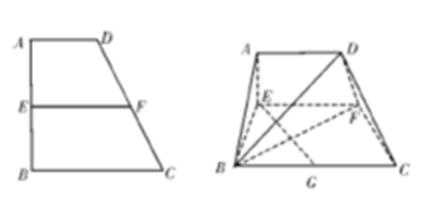如图,在





(1)边
(2)

正确答案
见解析。
解析
解:由

所以,
由正弦定理 
(2)
由余弦定理:
知识点
已知点



(1)求点

(2)过点





正确答案
见解析
解析
(1)依题意得


所以


(2)△
证明:
(a)当直线

代入




------------------3分
(b)当直线







设




-----------------8分

综上,△
知识点
已知函数

①





正确答案
②、③
解析
略
知识点
如图,已知




正确答案
解析
略
知识点
17.已知梯形A
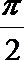
(1)当x=2时,求证:BD⊥EG;
(2)若以F、B、c、D为顶点的三棱锥的体积记为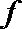
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析