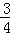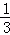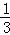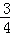- 不等式恒成立问题
- 共92题
设a，b∈R，若x≥0时恒有0≤x4－x3＋ax＋b≤(x2－1)2，则ab＝__________.
正确答案
－1
解析
令x＝1，得0≤1－1＋a＋b≤0，
整理，得a＋b＝0，①
令x＝－1，得0≤1－(－1)－a＋b≤0，
整理，得a－b＝2，②
解①②组成的方程组，得
∴ab＝－1
知识点
设
正确答案
解析
略
知识点
设z＝x＋2y，其中实数x，y满足
正确答案
［0，
解析
不等式组表示的可行域如图阴影部分，
结合图象知，O点，C点分别使目标函数取得最小值、最大值，代入得最小值为0，最大值为
知识点
已知f（x）为偶函数，当x≥0时，f（x）=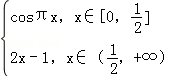
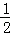
A[
B[﹣
C[
D[﹣
正确答案
解析
当x∈[0，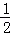
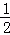
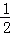
则πx=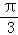
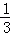
当x＞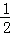
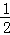
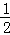
解得x=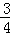
则当x≥0时，不等式f（x）≤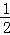
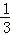
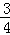
则由f（x）为偶函数，
∴当x＜0时，不等式f（x）≤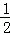
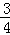
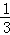
即不等式f（x）≤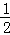
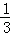
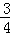
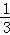
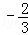
则由﹣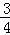
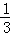
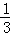
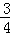
解得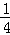
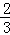
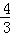
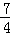
即不等式f（x﹣1）≤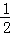
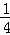
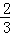
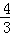
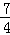
故选：A。
知识点
已知f(x)＝|ax＋1|(a∈R)，不等式f(x)≤3的解集为{x|－2≤x≤1}。
(1)求a的值；
(2)若
正确答案
(1)2； (2) k≥1
解析
(1)由|ax＋1|≤3得－4≤ax≤2。
又f(x)≤3的解集为{x|－2≤x≤1}，所以当a≤0时，不合题意。
当a＞0时，
(2)记h(x)＝f(x)－
则
所以|h(x)|≤1，因此k≥1
知识点
扫码查看完整答案与解析