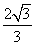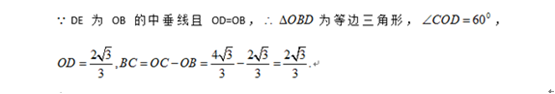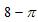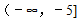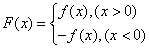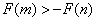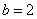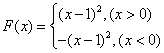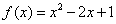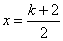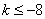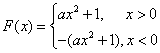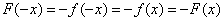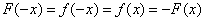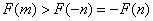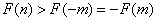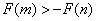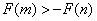- 不等式恒成立问题
- 共92题
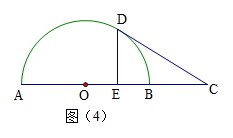
如图(4),AB是半圆的直径,C是AB
延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,
且E是OB的中点,则BC的长为 。
正确答案
解析
知识点
已知D是由不等式组


正确答案

解析
略
知识点
设函数

(1)求
(2)若


正确答案
(1)2(2)
解析
解析:(1)由题意,对任意


………………2分
即

因为

解法二:因为




当



所以

(2)由(1)知



………………6分
当



………………7分
由

因为

因为




所以△
解得
所以,的取值范围是
知识点
已知实数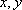
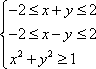
正确答案
解析
略
知识点
已知函数f(x)=log2(|x﹣1|+|x+2|﹣a)。
(1)当a=7时,求函数f(x)的定义域;
(2)若关于x的不等式f(x)≥3的解集是R,求实数a的取值范围。
正确答案
(1)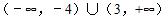
解析
(1)由题设知:|x﹣1|+|x+2|>7,
不等式的解集是以下不等式组解集的并集: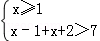
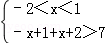
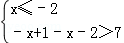
解得函数f(x)的定义域为(﹣∞,﹣4)∪(3,+∞); …(5分)
(2)不等式f(x)≥3,即|x﹣1|+|x+2|≥a+8,
∵x∈R时,恒有|x﹣1|+|x+2|≥|(x﹣1)﹣(x+2)|=3,…(8分)
∵不等式|x﹣1|+|x+2|≥a+8解集是R,
∴a+8≤3,
∴a的取值范围是(﹣∞,﹣5], …(10分)
知识点
设函数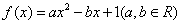
(1)若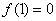
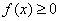
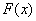
(2)在(1)在条件下,当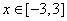
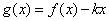
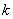
(3)设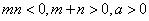
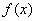

正确答案
见解析。
解析
(1)∵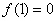
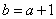
由于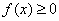
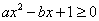
当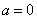
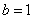
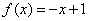
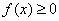
当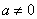
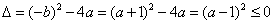
得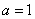
从而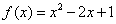
(2)由(1)知
∴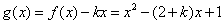
由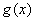
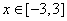
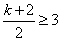
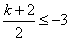
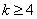
(3)∵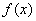
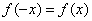
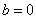
故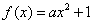
∵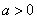
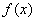
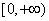
对于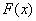
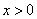
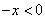
当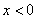
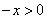
∴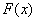
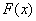
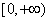
∵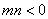
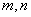
(1)当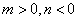
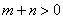
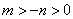
(2)当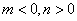
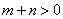
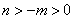
即
综上可知
知识点
若
正确答案
(﹣∞,﹣

解析
∵设f(x)=
则f′(x)=

∵x≥4,要使f(x)<0恒成立,需分3种情况:
①若m>0或m<﹣1,f′(x)>0,f(x)是增函数,f(4)=

解得:m<﹣1;
∴m<﹣1;
②若﹣1<m<0,f′(x)<0,f(x)是减函数,f(4)=
解得:﹣1<m<﹣

∴﹣1<m<﹣

③若m=﹣1,f(x)=
综上所述,m的取值范围是(﹣∞,﹣

知识点
已知函数
(1)若x<a时,f(x)<1恒成立,求实数a的取值范围;
(2)若a≥﹣4时,函数f(x)在实数集R上有最小值,求实数a的取值范围
正确答案
见解析。
解析
(1)因为x<a时,f(x)=4x﹣4×2x﹣a,所以令2x=t,则有0<t<2a,
所以f(x)<1当x<a时恒成立,可转化为
即
令

所以
所以

所以

所以
(2)当x≥a时,f(x)=x2﹣ax+1,即
①当
所以f(x)min=f(a)=1;
②当



所以由①②可得:当x≥a时有:
当x<a时,f(x)=4x﹣4×2x﹣a,令2x=t,t∈(0,2a),则
③当




④当

所以,此时,h(t)在(0,2a)上无最小值;
所以由③④可得当x<a时有:当

当
所以,由①②③④可得:
当


当
当﹣4≤a<0时,
综上所述,当


所以函数f(x)在实数集R上有最小值时,实数a的取值范围为
知识点
若点


正确答案
3
解析






知识点
已知函数
(1)若函数
(2)若函数
正确答案
见解析
解析
(1)
∵



即



又函数

(2)考查

∴



∵

①若








②若






③若








由
综上所述,
知识点
扫码查看完整答案与解析