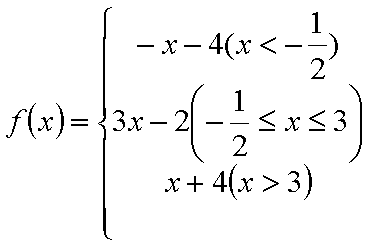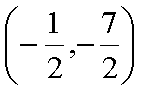- 不等式恒成立问题
- 共92题
已知函数
(1)当

(2)若关于



正确答案
(1)
解析
(1)由题设知:
不等式的解集是以下不等式组解集的并集:


解得函数

(2)不等式



不等式


知识点
设函数
(1) 求函数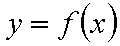
(2) 若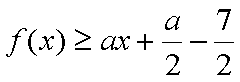
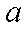
正确答案
见解析
解析
(1)由题意得
所以 f(x)在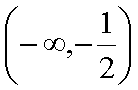
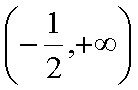
所以当
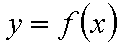
此时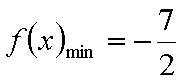
(2)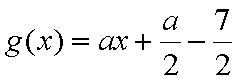
由图象可知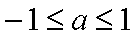
知识点
设函数
(1)当

(2)若


正确答案
见解析
解析
(1)



解得:

故不等式


(2)因为: 

所以
由题意得:


知识点
数列






(1)求数列
(2)若对任意的


正确答案
见解析
解析
(1)因为
所以

1、2得
又因为



(2)
所以



令
当



所以
知识点
已知椭圆

(1)求椭圆的方程;
(2)过A作直线与椭圆交于另外一点B,求ΔAOB面积的最大值。
正确答案
见解析
解析
解:(1)有已知:c = 2,

故椭圆方程为
(2)当AB斜率不存在时:
当AB斜率存在时:设其方程为:
由
由已知:
即:
O到直线AB的距离:
∴
∵


此时
综上所求:当AB斜率不存在或斜率为零时,ΔAOB面积取最大值为
知识点
已知
(1)当a=1时求不等式
(2)如果函数
正确答案
见解析。
解析
(1)
∴

(2)由

令


这两个函数的图象有两个不同的交点,
所以,函数
知识点
设f(x)=﹣cosx﹣sinx,f′(x)是其导函数,若命题“∀x∈[
正确答案
解析


知识点
一个几何体的三视图如图所示,则该几何体的表面积为( ).
正确答案
解析
由三视图可知该几何体是底面为直角梯形(梯形上底为1,下底为2,直角腰为
1),高为1的直棱柱,故其表面积为

知识点
如图所示,三棱柱ABC—A1B1C1中,AB=AC=AA1=2,面ABC1上面AAlClC,∠AAlCl=∠BAC1=600,AC1与A1C相交于0,E为BC的中点。
(1)求证.OE∥面AAl BlB;
(2)求证:B0⊥面AA1C1C;
(3)求三棱锥C—AEC1的体积。
正确答案
见解析。
解析



∴
∴
(2)由条件知,四边形ACC1A1为菱形
∠AA1C1=60°,∴A1C=2 ,ΔABC1中,AB=2,

∴BO⊥AC1 ,又平面
∴
(3)∵


知识点
若两个正实数



正确答案
解析







知识点
扫码查看完整答案与解析