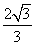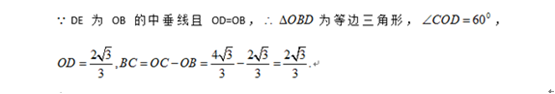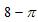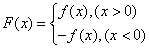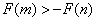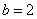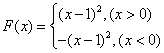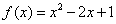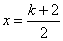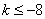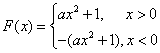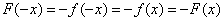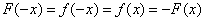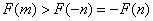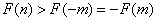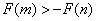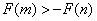- 不等式恒成立问题
- 共92题
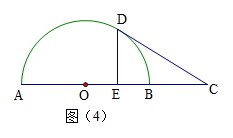
如图(4),AB是半圆的直径,C是AB
延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,
且E是OB的中点,则BC的长为 。
正确答案
解析
知识点
已知D是由不等式组


正确答案

解析
略
知识点
设函数

(1)求
(2)若


正确答案
(1)2(2)
解析
解析:(1)由题意,对任意


………………2分
即

因为

解法二:因为




当



所以

(2)由(1)知



………………6分
当



………………7分
由

因为

因为




所以△
解得
所以,的取值范围是
知识点
已知实数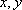
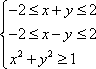
正确答案
解析
略
知识点
设函数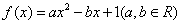
(1)若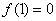
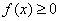
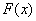
(2)在(1)在条件下,当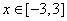
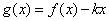
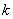
(3)设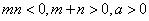
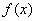

正确答案
见解析。
解析
(1)∵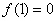
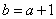
由于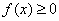
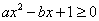
当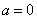
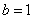
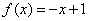
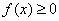
当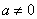
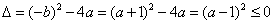
得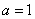
从而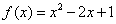
(2)由(1)知
∴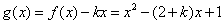
由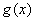
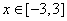
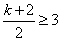
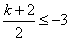
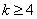
(3)∵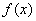
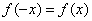
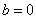
故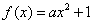
∵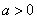
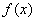
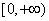
对于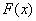
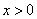
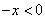
当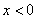
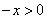
∴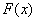
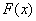
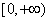
∵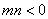
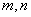
(1)当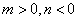
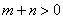
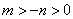
(2)当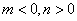
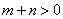
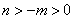
即
综上可知
知识点
扫码查看完整答案与解析