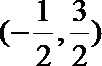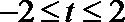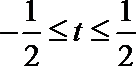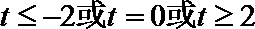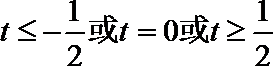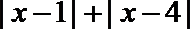不等式恒成立问题
共92题

· 不等式恒成立问题

不等式恒成立问题
共92题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 18 分

23．已知函数．

（1）作出函数的图像，并求当时恒成立的取值范围；

（2）关于的方程有解，求实数的取值范围；

（3）关于的方程（）恰有6个不同的实数解，求的取值范围．

正确答案

（1）解：

（作图如下：）

已知当时，即

（2），令，则

即方程上有解

当时，

（3）关于的方程（）恰有6个不同的实数解即有6个不同的解，

数形结合可知必有和，

令，则关于的方程有一根为2，另一根在间

解析

解析已在路上飞奔，马上就到！

知识点

函数零点的判断和求解不等式恒成立问题绝对值不等式的解法

题型：填空题

填空题 · 5 分

13．若对任意x>0，≤a恒成立，则a的取值范围是________．

正确答案

[，＋∞）

解析

因为x>0，所以，当且仅当即时等号成立，故a的取值范围是，即

知识点

不等式恒成立问题

题型：填空题

填空题 · 4 分

15．若关于的不等式对任意恒成立，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题

题型：填空题

填空题 · 4 分

15．已知是偶函数，当时，，且当时，恒成立，则的最小值是___________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的性质不等式恒成立问题

题型：简答题

简答题 · 13 分

20．已知．

（Ⅰ）当时,判断的奇偶性,并说明理由；

（Ⅱ）当时,若,求的值；

（Ⅲ）若,且对任何不等式恒成立,求实数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数奇偶性的判断指数幂的运算不等式恒成立问题绝对值不等式的解法

题型：简答题

简答题 · 16 分

22.已知函数

(1)当时，解关于的不等式；

(2)函数在的最大值为，求正数的值；

(3)对于给定的正数，有一个最大的正数，使得在整个区间上，不等式恒成立. 求出的解析式

正确答案

（1）时，

由①得，，由②得，或，

∴为所求.

（2），

当时，，不合题意，

当时，

综上所述，

（3）∵，当，即时，

当，即时，

∴

解析

解析已在路上飞奔，马上就到！

知识点

二次函数在闭区间上的最值一元二次不等式的解法不等式恒成立问题

题型：填空题

填空题 · 4 分

11．在R上定义运算△：x△y=x（1 -y）若不等式（x-a）△（x+a）<1，对任意实数x恒成立，则实数a的取值范围是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题

题型：单选题

单选题 · 5 分

6．设奇函数在上是增函数，且，若函数对所有的都成立，则当时t的取值范围是（）

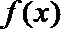
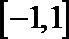
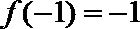
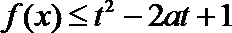
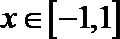
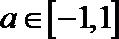
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

奇偶性与单调性的综合不等式恒成立问题

题型：简答题

简答题 · 12 分

19. 已知函数。

（Ⅰ）求函数在上的值域；

（Ⅱ）若对于任意的，不等式恒成立，求。

正确答案

（Ⅰ），

∵，∴，∴，

∴，即函数在上的值域是[－3，3] ．

（Ⅱ）∵对于任意的，不等式恒成立，

∴是的最大值，∴由，

解得∴．

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值正弦函数的定义域和值域三角函数中的恒等变换应用不等式恒成立问题

题型：简答题

简答题 · 12 分

16．设表示幂函数在上是增函数的的集合；Q表示不等式对任意恒成立的的集合。

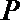
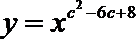
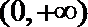
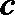
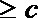
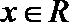
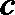
（1）求；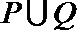

（2）试写出一个解集为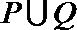的不等式。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

并集及其运算函数单调性的性质不等式恒成立问题

继续学习学习下一知识点

下一知识点 : 分式不等式的解法

百度题库 > 高考 > 文科数学 > 不等式恒成立问题

扫码查看完整答案与解析