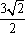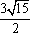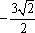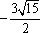- 函数的图象与图象变化
- 共221题
在平面直角坐标系中,定义两点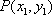
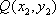

(1)若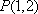
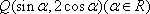
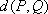
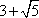
(2)若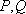
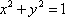
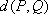
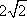
(3) 若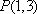
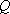
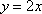
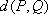

其中为真命题的是
正确答案
解析
略
知识点
已知函数
(1) 求函数
(2) 已知

正确答案
见解析。
解析
知识点
已知点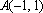
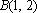
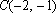
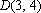
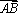
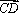
正确答案
解析
略
知识点
设函数





正确答案
解析
略
知识点
在复平面内,复数 
正确答案
解析
略
知识点
如图,设区域


正确答案
解析
略
知识点
已知函数

(1)求
(2)曲线





正确答案
(1)



(2)
解析
(1)
(1)当



(2)当


令

令
∴


在
(2)∵

∴曲线


即
∴
∴
由(1)知,
(i)当


(ii)当



此时题设成立等价条件是

即:
即:

解得:
由(i)(ii)可知

知识点
已知 


正确答案
解析
略
知识点
已知函数

正确答案
解析
略
知识点
已知

正确答案
解析
略
知识点
扫码查看完整答案与解析