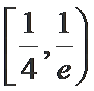- 函数的图象与图象变化
- 共221题
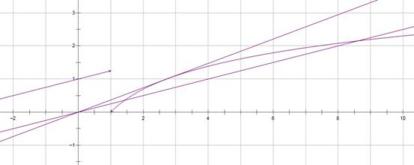
13．已知函数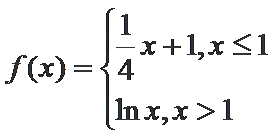
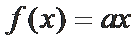
取值范围是___________
正确答案
解析
∵
∴
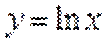
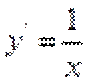
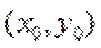
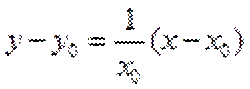
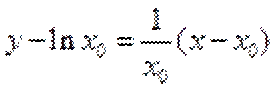
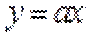
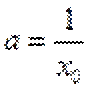
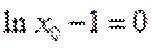
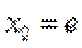
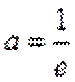
当直线与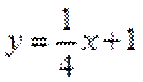
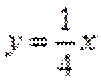
当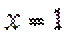
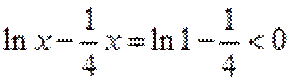
当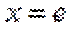
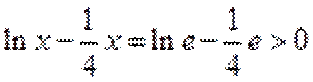
当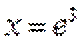
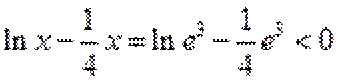
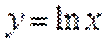
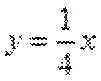
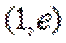
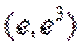
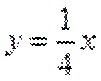
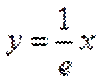
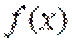
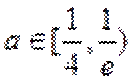
考查方向
解题思路
本题考查运用导数解决函数的能力，解题步骤如下： 先求导，找函数的切线方程，再利用零点的判定方法，找到a的取值范围。
易错点
本题必须注意审题，忽视则会出现错误。
知识点
11．如图（3）所示，侧棱与底面垂直，且底面为正方形的四棱柱ABCD－A1B1C1D1中，AA1＝2，AB＝1，M、N分别在AD1、BC上移动，始终保持MN∥平面DCC1D1，设BN＝x，MN＝y，则函数y＝f（x）的图像大致是（ ）
A
B
C
D
正确答案
解析
在
因此A选项不正确，B选项不正确，D选项不正确，所以选C选项。
考查方向
解题思路
先根据MN∥平面DCC1D1构造出点E,通过相似比求出ME，从而找到x,y之间的关系式。因此A选项不正确，B选项不正确，D选项不正确，所以选C选项。
易错点
易忽视x的取值范围。
知识点
4．要得到函数
A向左平移
B向右平移
C向右平移
D向左平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．当
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．为了得到函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知函数
A向右平移
B向右平移
C向左平移
D向左平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8. 设函数
A
B
C
D
正确答案
解析
解：∵f（x）=xsinx+cosx，
∴f'（x）=（xsinx）'+（cosx）'
=x（sinx）'+（x）'sinx+（cosx）'
=xcosx+sinx-sinx
=xcosx，
∴k=g（t）=tcost，
根据y=cosx的图象可知g（t）应该为奇函数，且当x＞0时g（t）＞0.
故选B．
考查方向
利用导数研究函数的单调性．
解题思路
先对函数f（x）进行求导运算，根据在点（t，f（t））处切线的斜率为在点（t，f（t））处的导数值，可得答案．
易错点
①判断g（t）=tcost为奇函数；
②判断当x＞0时g（t）＞0.
教师点评
本题主要考查函数的导数和在某点处切线斜率的关系．属基础题．
知识点
11．如图，在平面直角坐标系中，AC平行于x轴，四边形ABCD是边长为1的正方形，记四边形位于直线x＝t(t＞0)左侧图形的面积为f(t)，则f(t)的大致图象是 ( )．
A
B
C
D
正确答案
解析
当
考查方向
本题主要考查了实际问题对应的函数图象问题,在近几年的各省高考题出现的频率较高，常与长度、面积、体积为背景。
易错点
1、不理解图象代表的意义。
2、解决问题的切入点不合理或找不到切入点。
知识点
14. 某食品的保鲜时间t（单位：小时）与储藏温度x（恒温，单位：
正确答案
4 是
解析
由该食品在
考查方向
解题思路
由该食品在
易错点
对于第二问不能灵活处理题目信息进行试算明确得出正确结论出错。
知识点
扫码查看完整答案与解析