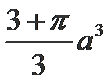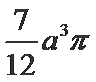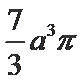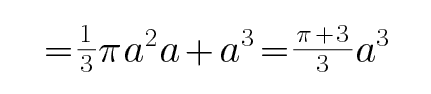- 由三视图还原实物图
- 共40题
15.某组合体的三视图如图2示，则该几何体的体积为 .
正确答案
解析
依题意知，该几何体是上面长方体下接半圆柱的组合体，故其体积
为：
考查方向
解题思路
1.先根据三视图还原成原来的几何体；2.根据体积公式求出该几何体的体积。
易错点
1.不会根据三视图还原原来的几何体形状；
2.记不住圆柱的体积公式导致结果出错。
知识点
A
B
C
D
正确答案
解析
最长的棱为
考查方向
解题思路
根据题中条件画出还原的几何体，如图所示.
易错点
没有正确的分析图中的位置关系与数量关系，将三视图还原错误
知识点
10.某几何体的三视图（单位：
几何体的表面积是 ▲ 
正确答案
解析
将三视图还原成直观图，如图所示，
S=3
考查方向
解题思路
将三视图还原成直观图，半个正方体直接计算表面积和体积
易错点
本题易在求表面积出错
知识点
3．如图为一个半球挖去一个圆锥后的几何体的三视图，则剩余部分与挖去部分的体积之比为（ ）
A
B
C
D
正确答案
解析
由三视图可得，半球的半径为2，圆锥的底面半径和高都等于2，所以半球的体积为
考查方向
解题思路
由三视图先分别求出半球和圆锥的体积，再求出剩余部分的体积，即可求出体积比。
易错点
本题易在求半球的体积时发生错误。
知识点
7．某三棱锥的三视图如图所示，则该三棱锥的体积是
A
B
C
D
正确答案
解析
三棱锥如下图所示：
CD＝1，BC＝2，CD⊥BC，
且三棱锥A－BCD的高为1
底面积SBCD＝
故选A。
考查方向
解题思路
由三视图知该几何体为如图所示的三棱锥。用三棱锥的体体积公式计算成即可。
易错点
本题在几何体的还原成平面直观图上易出问题，从而导致体积计算出错。
知识点
3．如图为一个半球挖去一个圆锥后的几何体的三视图，则剩余部分与挖去部分的体积之比为（ ）
A
B
C
D
正确答案
解析
由三视图可得，半球的半径为2，圆锥的底面半径和高都等于2，所以半球的体积为
考查方向
解题思路
由三视图先分别求出半球和圆锥的体积，再求出剩余部分的体积，即可求出体积比。
易错点
本题易在求半球的体积时发生错误。
知识点
11.如右下图所示为某几何体形状的纸盒的三视图，在此纸盒内放一个小正四面体，若小正四面体在纸盒内可以任意转动，则小正四面体的
A
B
C
D
正确答案
解析
有几何体三视图可知，该纸盒为棱长为
考查方向
解题思路
先讲几何体的三视图，还原成立体图形，得到该纸盒为棱长为
易错点
1. 三视图还原直观图2.不能正确理解“在此纸盒内放一个小正四面体，若小正四面体在纸盒内可以任意转动”3. 球与正四面体的切接关系(位置关系与数量关系)
知识点
8．若圆
A
B
C
D
正确答案
解析
只需求圆心（0，1）到曲线
距离
所以，若圆与曲线无公共点，则0＜ r＜
故选C。
考查方向
解题思路
先根据题意取曲线上的点
易错点
本题易在理解题意上出现错误。本题易在用变量得到距离后，求最值时极易出错。
知识点
4.如图为某几何体的三视图，则该几何体的表面积为（ ）
A
B
C
D
正确答案
解析
从三视图看，该几何体由两部分组成。左边部分为半个圆柱，圆柱的高为2，上下底面均为全等的半圆、半径为1；右边部分为正方体，棱长为2.右边部分正方体的表面积为5个侧面
考查方向
本题考查三视图、表面积的计算，本质上考查的是空间想象能力。
解题思路
从三视图看，该几何体由两部分组成。左边部分为半个圆柱，圆柱的高为2，上下底面均为全等的半圆、半径为1；右边部分为正方体，棱长为2.
易错点
对左边部分的还原，注意应为”半个圆柱“，同时也易错误地把半个圆柱与正方体共同的一个侧面面积也算进去。
教师点评
解三视图问题，一定要注意还原原几何体，一般为组合体。还原后，注意再去对应的检查，看是否与题中所给的三视图一致。在计算表面积的时候，注意只是表面的面积，如果把不是在表面的面积算进去，则会出错。
知识点
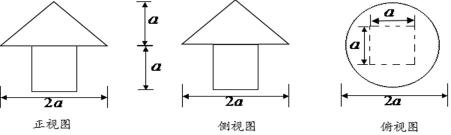
几何体的三视图如下，则它的体积是（ ）
A
B
C
D
正确答案
解析
故选择：A .
考查方向
考查集合体三视图的理解，三视图还原成简单集合体求体积。
解题思路
根据三视图展开想象还原成空间立体图形；再根据组成几何体的各种规则图形公式求出体积：图中的几何体的体积= 圆锥体积+正方体体积。
易错点
没有形成空间想象力，未能将三视图还原成原几何体。
教师点评
要求学生熟悉圆锥和正方体的几何，塑造学生的空间思维能力和空间想象力。
知识点
扫码查看完整答案与解析