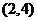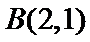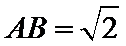- 一元二次不等式的解法
- 共69题
1. 设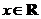
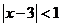
正确答案
知识点
2.设变量


正确答案
解析
作出不等式组对应的平面区域如图:(阴影部分).由z=3x+y得y=-3x+z,平移直线y=-3x+z,由图象可知当直线y=-3x+z经过点A时,直线y=-3x+z的截距最大,此时z最大.,当 
考查方向
解题思路
线性规划也是高考中常考的知识点,一般以客观题形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有:纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合,准确作出图形是解决问题的关键
易错点
根据题意正确作出约束条件对应的平面区域图象.
知识点
12.已知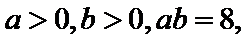
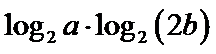
正确答案
4
解析
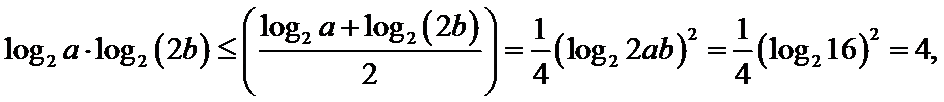
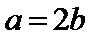
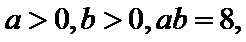
考查方向
解题思路
在利用基本不等式求最值时,一定要紧扣“一正、二定、三相等”这三个条件,注意创造“定”这个条件时常要对所给式子进行拆分、组合、添加系数等处理,使之可用基本不等式来解决,若多次使用基本不等式,必须保持每次取等的一致性.
易错点
不等式取等号的条件
知识点
4. 若平面区域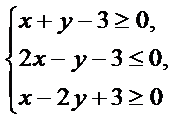
正确答案
解析
画出不等式组的平面区域如题所示,由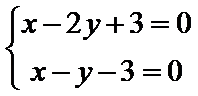
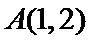
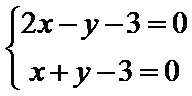
由题意知,当斜率为1的两条直线分别过点A和点B时,两直线的距离最小,即
考查方向
解题思路
画出可行域,利用垂直性质和两点间距离公式求出
易错点
对可行性区域的划分出现错误
知识点
5.函数
正确答案

解析



考查方向
解题思路
列出满足要求的不等式,利用不等式求解
易错点
列出所有满足要求的不等式
知识点
11.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额表所示,如果生产1吨甲乙产品可获利润分别为3万元.4万元,则该企业每天可获得最大利润为( )
正确答案
解析
设该企业每天生产甲乙两种产品分别

由题意可列
当直线



故答案选
考查方向
解题思路
本题主要考查的是线性规划,属于容易题.线性规划类问题的解题关键是先正确画出不等式组所表示的平面区域,然后确定目标函数的几何意义,通过数形结合确定目标函数何时取得最值.解题时要看清楚是求“最大值”还是求“最小值”,否则很容易出现错误;画不等式组所表示的平面区域时要通过特殊点验证,防止出现错误.
易错点
可行域作图及目标函数的正确
知识点
11.不等式
正确答案
解析
试题分析:由




考查方向
解题思路
利用解一元二次不等式的方法直接计出即可。
易错点
注意二次项的系数为负。
知识点
14.设




正确答案
解析
求出M的最小值为-2,N的最大值为2,则
考查方向
解题思路
本题考查简单的线性规划问题分别计算出M,N的最小值和最大值即可。
易错点
最值点找错。
知识点
6.已知



正确答案
解析
根据题意,可知
由图可知:目标函数在点(2,2)处取得最大值为
考查方向
线性规划,平面向量的数量积
解题思路
根据题意作出可行域,然后求得目标函数的最值点
易错点
作图错误,找不到最值点
知识点
11.不等式
正确答案
解析
由




知识点
扫码查看完整答案与解析